 |
A C. 1218. feladat (2014. március) |
C. 1218. Egy 80 cm sugarú körasztalon a négyzet alakú terítő félrecsúszott. A terítő egyik sarka pontosan az asztal szélére került, és az ezzel szemközti csúcsra illeszkedő két oldala érinti az asztal szélét. Adjuk meg a terítő oldalának hosszát milliméter pontossággal.
(5 pont)
A beküldési határidő 2014. április 10-én LEJÁRT.
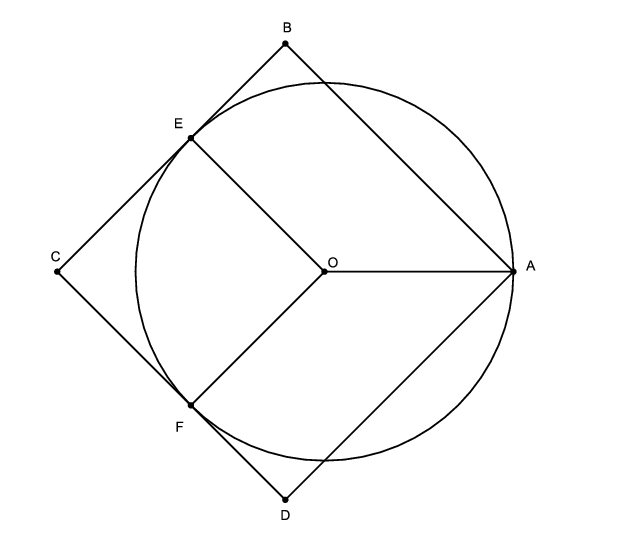
Megoldás. A terítő négy sarkát jelölje \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\), az illeszkedő csúcs legyen az \(\displaystyle A\), a \(\displaystyle BC\) a kört érintse \(\displaystyle E\)-ben, a \(\displaystyle DC\) pedig \(\displaystyle F\)-ben, a kör középpontját pedig jelölje \(\displaystyle O\). Mivel egy érintő merőleges az érintési pontba húzott sugárra, ezért az \(\displaystyle OECF\) négyszög \(\displaystyle E\), \(\displaystyle C\) és \(\displaystyle F\) csúcsánál derékszög van, valamint \(\displaystyle OE=OF=r\), tehát a négyszög négyzet. Így az \(\displaystyle OEC\) háromszög egyenlőszárú, a szárak hossza \(\displaystyle r\), ezért \(\displaystyle OC=r\sqrt2\). A szimmetria miatt \(\displaystyle C\), \(\displaystyle O\) és \(\displaystyle A\) egy egyenesen vannak, tehát \(\displaystyle AC=r+r\sqrt2\). Mivel \(\displaystyle AB=\frac{AC}{\sqrt2}\), ezért \(\displaystyle AB=\frac{r+r\sqrt2}{\sqrt2}=\frac{r}{\sqrt2}+r=\frac{80}{\sqrt2}+80\approx136,6~{\rm (cm)}\).
Statisztika:
104 dolgozat érkezett. 5 pontot kapott: Brányi Balázs, Horváth 016 Gábor, Kardos Bálint Tamás, Knoch Júlia, Kocsis Júlia, Kovács 246 Benedek, Papp 535 Ágnes, Polgár Márton, Radnai Bálint, Révy Gábor, Szécsi Adél Lilla, Széles Katalin, Szemerédi Levente, Zsakó Ágnes. 4 pontot kapott: Bodonhelyi Anna, Bottlik Judit, Döbröntei Dávid Bence, Ghyczy András, Györök Lídia, Hegedűs Henrietta, Kerekes Anna, Kis 913 Levente, Klász Viktória, Kovács 526 Tamás, Kovács Kristóf, Kovács Péter Tamás, Molnár-Sáska Zoltán, Pap-Takács Mónika, Ratkovics Gábor, Sándor Gergely, Schefler Barna, Szűcs 324 Ágnes, Vágó Richárd. 3 pontot kapott: 15 versenyző. 2 pontot kapott: 20 versenyző. 1 pontot kapott: 28 versenyző. 0 pontot kapott: 8 versenyző.
A KöMaL 2014. márciusi matematika feladatai

