A C. 1288. feladat (2015. április)

C. 1288. Az \(\displaystyle ABCD\) paralelogramma \(\displaystyle AB\) oldalának a \(\displaystyle B\) csúcshoz közelebb eső harmadolópontja \(\displaystyle H\), a \(\displaystyle BC\) oldal felezőpontja pedig \(\displaystyle F\). Milyen arányban osztja az \(\displaystyle AF\) és \(\displaystyle DH\) szakaszok metszéspontja ezeket a szakaszokat?

(5 pont)

A beküldési határidő 2015. május 11-én LEJÁRT.

Megoldás. Jelölje az \(\displaystyle AF\) és a \(\displaystyle DH\) szakaszok metszéspontját \(\displaystyle K\), az \(\displaystyle AB\) oldal felezőpontját \(\displaystyle N\), a \(\displaystyle BC\) oldal \(\displaystyle B\)-hez közelebbi negyedelőpontját pedig \(\displaystyle J\). Húzzunk párhuzamost \(\displaystyle H\)-n és \(\displaystyle N\)-en keresztül \(\displaystyle BC\)-vel, \(\displaystyle J\)-n és \(\displaystyle F\)-en keresztül pedig \(\displaystyle AB\)-vel. Az oldalakkal vett metszéspontokat az ábra szerint jelöljük. Ekkor \(\displaystyle M\) a \(\displaystyle CD\) oldal felezőpontja, \(\displaystyle G\) pedig a \(\displaystyle C\)-hez közelebbi harmadolópontja lesz; \(\displaystyle I\) az \(\displaystyle AD\) oldal \(\displaystyle A\)-hoz közelebbi negyedelőpontja, \(\displaystyle E\) pedig a felezőpontja.

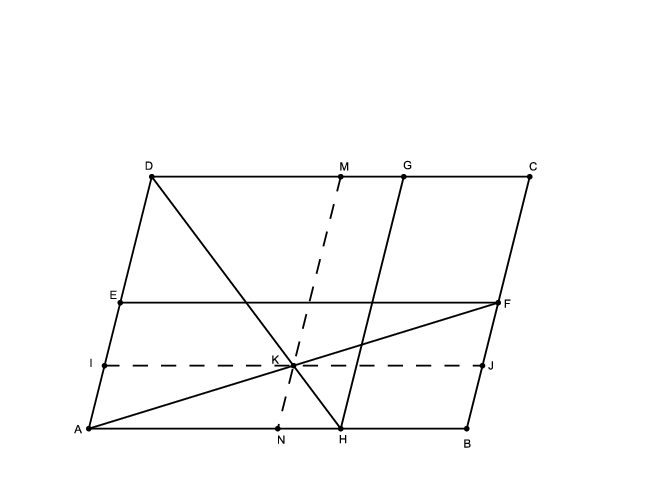
Azt sejtjük, hogy \(\displaystyle K\) felezi az \(\displaystyle AF\) szakaszt, és negyedeli a \(\displaystyle DH\) szakaszt. Ha belátjuk, hogy \(\displaystyle AF\) felezőpontja és \(\displaystyle DH\)-nak a \(\displaystyle H\)-hoz közelebbi negyedelőpontja egyaránt illeszkedik az \(\displaystyle MN\) és a \(\displaystyle IJ\) szakaszra, azzal belátjuk, hogy ez a két pont egybeesik, vagyis ez a \(\displaystyle K\) metszéspont, és a kérdezett arányt is bizonyítjuk egyben.

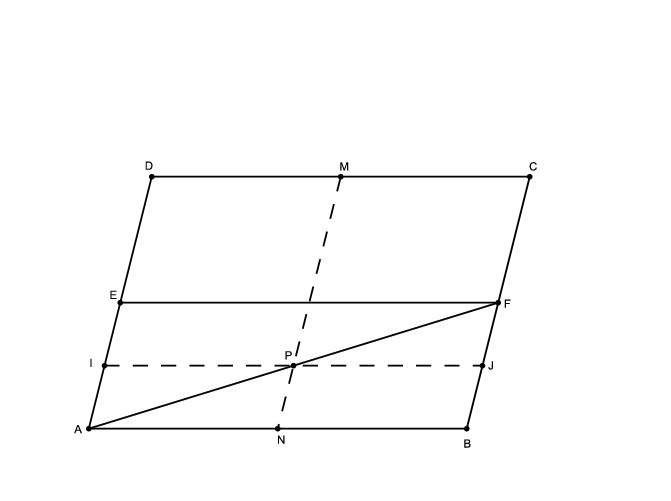
Tekintsük először az \(\displaystyle AF\) szakasz \(\displaystyle P\) felezőpontját. Az \(\displaystyle ABFE\) paralelogramma \(\displaystyle AF\) átlójának felezőpontján átmegy mindkét középvonal, vagyis az \(\displaystyle IJ\) és az \(\displaystyle NM\) szakasz is (hiszen az \(\displaystyle ABCD\) és az \(\displaystyle ABFE\) paralelogrammáknak az \(\displaystyle AB\) oldal felezőpontjára illeszkedő középvonal egyenese megegyezik).

Vizsgáljuk meg a \(\displaystyle DH\) szakasz \(\displaystyle H\)-hoz közelebbi \(\displaystyle S\) negyedelőpontját.

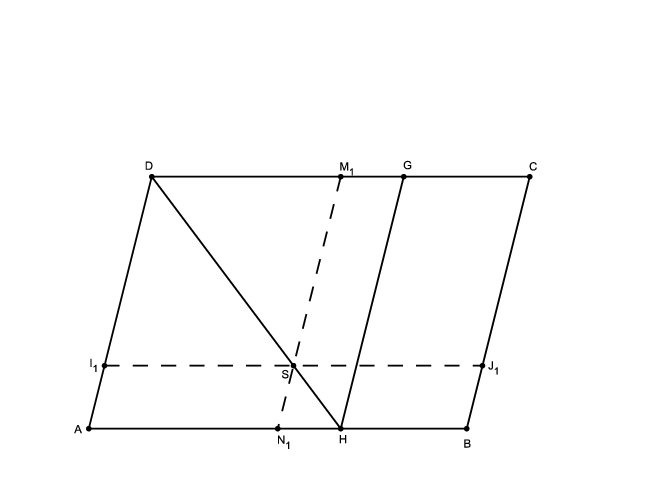
Az \(\displaystyle S\)-en keresztül \(\displaystyle AB\)-vel húzott párhuzamos \(\displaystyle BC\)-vel, illetve \(\displaystyle AD\)-vel vett metszéspontját jelölje rendre \(\displaystyle J_1\) és \(\displaystyle I_1\). Az \(\displaystyle S\)-en keresztül \(\displaystyle BC\)-vel húzott párhuzamos pedig az \(\displaystyle N_1\), illetve az \(\displaystyle M_1\) pontban metszi az \(\displaystyle AB\) és a \(\displaystyle CD\) szakaszt.

\(\displaystyle AHD\triangle\sim I_1SD\triangle\), ezért \(\displaystyle \frac{DI_1}{DA}=\frac{DS}{DH}=\frac34\), ami azt jelenti, hogy \(\displaystyle I_1\) az \(\displaystyle AD\) oldal \(\displaystyle A\)-hoz közelebbi negyedelőpontja, vagyis \(\displaystyle I_1\equiv I\). Tehát \(\displaystyle S\) illeszkedik \(\displaystyle IJ\)-re.

\(\displaystyle DSM_1\triangle\sim DHG\triangle\), amiből \(\displaystyle \frac{DM_1}{DG}=\frac{DS}{DH}=\frac34\), vagyis \(\displaystyle M_1\) a \(\displaystyle DG\) szakasz \(\displaystyle G\)-hez közelebbi negyedelőpontja. Mivel \(\displaystyle G\) harmadolópont, ezért \(\displaystyle DG=\frac23 DC\), és így \(\displaystyle DM_1=\frac34\cdot\frac23 DC=\frac12DC\), vagyis \(\displaystyle M_1\) a \(\displaystyle DC\) oldal felezőpontja, és így \(\displaystyle M_1\equiv M\). Tehát az \(\displaystyle S\) pont illeszkedik az \(\displaystyle MN\) szakaszra is.

Ezzel a bizonyítást befejeztük, a \(\displaystyle K\) metszéspont felezi az \(\displaystyle AF\) szakaszt, és egyben a \(\displaystyle DH\) szakasz \(\displaystyle H\)-hoz közelebbi negyedelőpontja.

Statisztika:

86 dolgozat érkezett.
5 pontot kapott:	59 versenyző.
4 pontot kapott:	11 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	8 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2015. áprilisi matematika feladatai