 |
A C. 1642. feladat (2020. december) |
C. 1642. Az \(\displaystyle ABCDEF\) konvex hatszög szemközti oldalai párhuzamosak, a három párhuzamos oldalpár egymástól való távolsága megegyezik, és az \(\displaystyle A\) és \(\displaystyle D\) csúcsánál derékszög van. Bizonyítsuk be, hogy a \(\displaystyle BE\) és \(\displaystyle CF\) átlók által bezárt szög \(\displaystyle 45^{\circ}\).
(5 pont)
A beküldési határidő 2021. január 11-én LEJÁRT.
Megoldás. A hatszögben az \(\displaystyle AB, DE\) és \(\displaystyle CD, FA\) oldalpárok egymással szemben helyezkednek el és a párok tagjai párhuzamosak egymással. Ebből, és az \(\displaystyle A\), illetve \(\displaystyle D\) csúcsnál levő derékszögekből az következik, hogy az \(\displaystyle AB\) és \(\displaystyle CD\), valamint \(\displaystyle DE\) és \(\displaystyle FA\) egyenesek merőlegesen metszik egymást, rendre az \(\displaystyle X\) és \(\displaystyle Y\) pontokban.
Ez azt is jelenti, hogy az \(\displaystyle ABCDEF\) konvex hatszög kiegészíthető az \(\displaystyle AXDY\) téglalappá.
Legyen a \(\displaystyle BE\) és \(\displaystyle CF\) átlók metszéspontja \(\displaystyle M\). Húzzunk merőlegeseket a hatszög szemben levő oldalaira az \(\displaystyle M\) ponton keresztül. Jelöléseinket az ábrán láthatjuk.
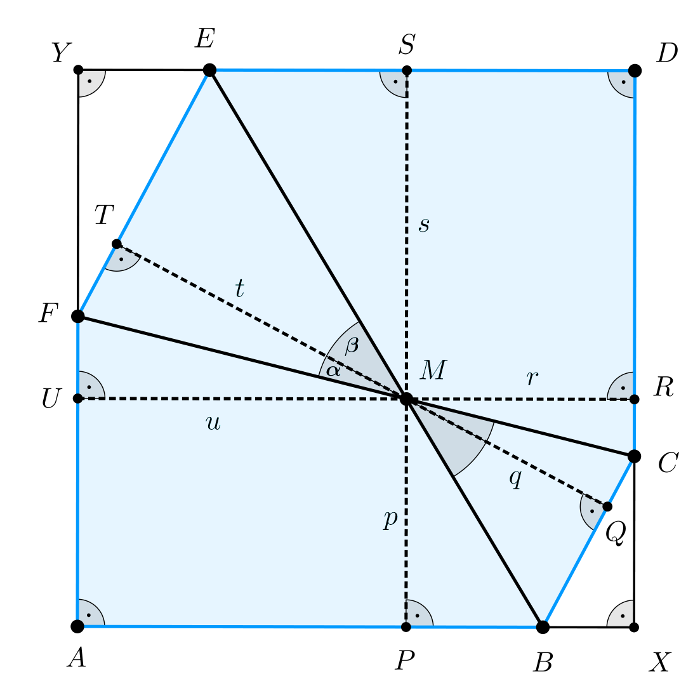
A szemközti oldalak párhuzamossága miatt az \(\displaystyle SM\), \(\displaystyle MP\); \(\displaystyle RM\), \(\displaystyle MU\); illetve a \(\displaystyle QM\), \(\displaystyle MT\) szakaszok egymás meghosszabbításai, vagyis az \(\displaystyle SP\) \(\displaystyle RU\) és \(\displaystyle QT\) szakaszok átmennek az \(\displaystyle M\) ponton. A feltételek között szerepelt az is, hogy a párhuzamos oldalpárok egymástól való távolsága megegyezik. Az utóbbi feltétel miatt \(\displaystyle PS=RU=QT\), így az ábra jelöléseivel
| \(\displaystyle (1)\) | \(\displaystyle p+s=r+u=q+t.\) |
A \(\displaystyle BC\) és \(\displaystyle EF\) oldalak párhuzamossága miatt a \(\displaystyle BCM\) és \(\displaystyle EFM\) háromszögek megfelelő szögei egyenlők, tehát a két háromszög hasonló. A háromszögek hasonlósága miatt teljesül az is, hogy két megfelelő oldal aránya megegyezik másik két megfelelő oldalhoz tartozó magasság arányával, vagyis \(\displaystyle \frac{CM}{FM}=\frac{q}{t}\).
A megfelelő szögek egyenlősége miatt a \(\displaystyle CRM\) és \(\displaystyle FUM\) derékszögű háromszögek is hasonlók, ezért \(\displaystyle \frac{CM}{FM}=\frac{r}{u}\).
Eszerint \(\displaystyle \frac{q}{t}=\frac{r}{u}\), amelyből azt kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle q=t\cdot{\frac{r}{u}}.\) |
Felhasználva az (1) egyenlőségből a \(\displaystyle q+t=r+u\) összefüggést, (2)-ből azt kapjuk, hogy \(\displaystyle t\cdot\left(\frac{r}{u}+1\right)=r+u\), vagy másként \(\displaystyle t\cdot\frac{r+u}{u}=r+u\), ahonnan a pozitív \(\displaystyle r+u\) tényezővel egyszerűsítve \(\displaystyle t=u\) adódik.
A \(\displaystyle TFM\) és \(\displaystyle FUM\) derékszögű háromszögekben az \(\displaystyle FM\) átfogó közös, \(\displaystyle t=u\) szerint pedig egy-egy befogójuk is egyenlő hosszúságú, ezért a két háromszög egybevágó, tehát az ábra jelöléseivel \(\displaystyle UMF\sphericalangle=\alpha\).
A megfelelő szögek egyenlősége alapján a \(\displaystyle PBM\) és \(\displaystyle SEM\) háromszögek is hasonlók, így a fentiekhez hasonlóan azt is könnyen bizonyíthatjuk, hogy \(\displaystyle s=t\). Ennek felhasználásával beláthatjuk, hogy az \(\displaystyle ETM\) és \(\displaystyle SEM\) derékszögű háromszögek egybevágók, ebből pedig azonnal következik, hogy \(\displaystyle EMS\sphericalangle=\beta\).
Eszerint \(\displaystyle UMS\sphericalangle=2\alpha+2\beta\), de mivel \(\displaystyle UM\) nyilvánvalóan merőleges \(\displaystyle SM\)-re, ezért \(\displaystyle 2\alpha+2\beta=90^{\circ}\), vagyis \(\displaystyle \alpha+\beta=45^{\circ}\), tehát a \(\displaystyle BE\) és \(\displaystyle CF\) átlók által bezárt szög valóban \(\displaystyle 45^{\circ}\)-os.
Megjegyzések:
1. A \(\displaystyle p+s=r+u\) összefüggésből az is következik, hogy \(\displaystyle AXDY\) négyzet, és a bizonyításból kiderül, hogy a \(\displaystyle PXRM\) és \(\displaystyle SYUM\) négyszögek is négyzetek.
2. Az ábrán jelölt derékszögű háromszögek közül a \(\displaystyle TFM\) és \(\displaystyle FUM\) mindig létrejön, mert ha nem így lenne, akkor a \(\displaystyle T\), \(\displaystyle F\), \(\displaystyle U\) pontok azonosak lennének, vagyis a hatszög \(\displaystyle F\) csúcsánál levő belső szöget az \(\displaystyle MF\) szakasz két egymás melletti derékszögre osztaná, de ez azt jelentené, hogy a hatszögben az \(\displaystyle F\) csúcshoz tartozó belső szög \(\displaystyle 180^{\circ}\)-os, ez pedig a feltételek mellett nyilván lehetetlen. Hasonlóan láthatjuk be az ábra többi derékszögű háromszögének létrejöttét.
Statisztika:
28 dolgozat érkezett. 5 pontot kapott: Andó Lujza, Biró 424 Ádám, Dobi Dorina Lili, Egyházi Hanna, Féger Tamás, Fekete András Albert, Horváth 828 Mátyás, Horváth Antal, Kadem Aziz, Kruppa László, Molnár Réka, Németh László Csaba, Németh Máté Előd, Schneider Anna, Szalanics Tamás, Téglás Panna. 4 pontot kapott: Fonyi Máté Sándor, Jakab Zsófi , Rátki Gergely. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. decemberi matematika feladatai

