 |
A C. 1644. feladat (2021. január) |
C. 1644. Egy keskeny, \(\displaystyle 10 \mathrm{cm} \times 30 \mathrm{cm}\) méretű, téglalap alakú tepsiben sütit sütöttünk, melynek a széle lett a legropogósabb. A sütit úgy vágjuk fel, hogy a vágások az oldalakkal párhuzamosan, végig futnak. Hány darabra osztható a sütemény, ha azt szeretnénk, hogy minden darabon ugyanakkora rész legyen a ropogós széléből?
(5 pont)
A beküldési határidő 2021. február 15-én LEJÁRT.
Megoldás. A feltétel szerint az kell, hogy a darabok mindegyike ugyanannyit tartalmazzon a téglalap kerületéből. Vizsgáljuk meg, hogy e feltétel mellett mely \(\displaystyle k,\ell\) értékekre lehetséges, hogy \(\displaystyle k\) vágás fut a hosszabb, 30 cm-es oldallal párhuzamosan és \(\displaystyle \ell\) vágás a rövidebb, 10 cm-es oldallal párhuzamosan. (Ekkor a részek száma \(\displaystyle (k+1)(\ell+1)\) lesz.)
Ha \(\displaystyle k\) és \(\displaystyle \ell\) mindegyike legalább 2, akkor van olyan rész, ami a széléből semmit sem tartalmaz, így ez nem lehetséges. Tehát \(\displaystyle k\) és \(\displaystyle \ell\) valamelyike 0 vagy 1. Ezt a négy esetet külön-külön vizsgáljuk.
1. eset: \(\displaystyle k=0\)
Ha \(\displaystyle \ell=0\), akkor a feltétel teljesül, tehát \(\displaystyle (k,\ell)=(0,0)\) lehetséges, ilyenkor 1 darab süti van.
Ha \(\displaystyle \ell=1\), akkor világos, hogy a rövidebb oldallal párhuzamos szimmetriatengely mentén kell vágni, ilyenkor két egybevágó szelet alakul ki, a feltétel teljesül, azaz \(\displaystyle (k,\ell)=(0,1)\) is lehet, ekkor 2 darab süti van.
Ha \(\displaystyle \ell\geq 2\), akkor a két szélső szelet tartalmaz egy-egy 10 cm-es oldalt, és ezen kívül még két-két szakaszt a hosszabbik 30 cm-es oldalakból. Ezen szakaszok hossza legyen \(\displaystyle (0<)x\) cm (világos, hogy a két szélső szeletnél ennek a szakasznak a hossza ugyanakkora kell legyen). (Lásd a lenti ábrát a szaggatott vonal nélkül.) Így tehát a két szélső szelet mindegyike összesen \(\displaystyle 10+2x\) cm szélt tartalmaz. A hosszabbik oldalakon fennmaradó két darab \(\displaystyle (30-2x)\) cm-es szél a maradék \(\displaystyle \ell-2\) vágással kialakított \(\displaystyle \ell-1\) részhez kerül, és a nekik jutó rész hossza is \(\displaystyle 10+2x\) kell legyen. Vagyis a \(\displaystyle 2(30-2x)=(\ell-1)(10+2x)\) egyenletnek kell teljesülnie. Az egyenletet átalakítva:
\(\displaystyle 60-4x=10(\ell-1)+2(\ell-1)x,\)
\(\displaystyle 60-10(\ell-1)=2(\ell+1)x.\)
Az egyenlet jobb oldalán pozitív érték áll, így \(\displaystyle \ell\leq 6\)-nak teljesülnie kell. Ha \(\displaystyle \ell\leq 6\), akkor az \(\displaystyle x=\frac{60-10(\ell-1)}{2(\ell+1)}\) választás megfelelő, és a két szélső vágás után csak arra kell figyelni, hogy vágások közötti távolságok egyformák legyenek. Tehát \(\displaystyle (k,\ell)\) lehet \(\displaystyle (0,2),\ (0,3),\ (0,4),\ (0,5),\ (0,6)\) is, ekkor a darabok száma rendre 3, 4, 5, 6, 7.
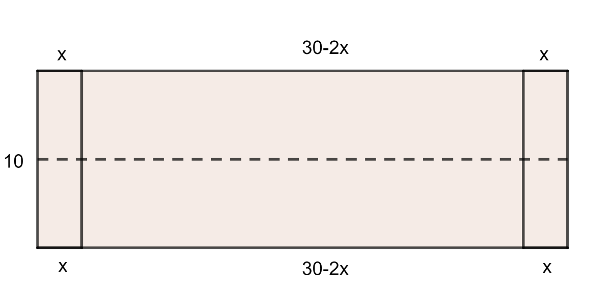
2. eset: \(\displaystyle k=1\)
Világos, hogy a hosszabb oldallal párhuzamos szimmetriatengelyen kell vágni a hosszabb oldallal párhuzamos 1 darab vágásnál. (Ugyanis a 10 cm-es oldal melletti két szelet ugyanannyi szélt tartalmaz a megfelelő 30 cm-es oldalból, ezért a 10 cm-es oldalból is ugyanannyit kell tartalmazniuk.)
Ezek szerint a szeletek a 30 cm-es vágásra tengelyesen szimmetrikusan helyezkednek el. Ha ezt a vágást (ami az ábrán szaggatott vonallal van jelölve) elhagynánk, akkor feleannyi szelet jönne létre (két-két szelet egybeolvad, mindegyik a tengelyes tükörképével), és egy megfelelő felosztást kapunk \(\displaystyle k=0\)-ra. Megfordítva, ha egy \(\displaystyle k=0\)-nál megfelelő felosztásnál még egy hosszabb oldallal párhuzamos, a középponton átmenő vágást csinálunk, akkor \(\displaystyle k=1\) mellett kapunk jó sütiosztást. Így az 1. eset alapján itt a megfelelő lehetőségek: \(\displaystyle (k,\ell)\) lehet \(\displaystyle (1,0),\ (1,1),\ (1,2),\ (1,3),\ (1,4),\ (1,5),\ (1,6)\) is, ekkor a darabok száma rendre 2, 4, 6, 8, 10, 12, 14.
3. eset: \(\displaystyle \ell=0\)
Csak az eddig nem vizsgált \(\displaystyle k\geq 2\) eseteket nézzük. Ekkor a két szélső (a 30 cm-es oldalhoz közelebbi) szeletnek több, mint 30 cm jut a kerületből, viszont van még legalább egy szelet, ami kevesebb mint 20 cm-t (a két 10 cm-es oldal egy-egy részét) kaphatja, így a feltétel biztosan nem teljesül.
4. eset: \(\displaystyle \ell=1\)
A 2. esethez hasonlóan itt is világos, hogy a rövidebb oldallal párhuzamos egyetlen vágást elhagyva egy megfelelő konfigurációt kapnánk \(\displaystyle \ell=0\) mellett (hiszen így két-két szelet alkot minden új szeletet). Mivel a 3. esetben nem kaptunk újabb megoldást (amire \(\displaystyle k\geq 2\)), ezért itt sem kapunk.
Tehát a darabok száma 1, 2, 3, 4, 5, 6, 7, 8, 10, 12 vagy 14 lehet.
Statisztika:
152 dolgozat érkezett. 5 pontot kapott: Ágoston Barbara, Atanaszov Hedvig, Bacsek Bálint , Barát Benedek, Barta Veronika, Beke Ambrus, Bencz Benedek, Besze Zsolt, Bettesch Helga Adél, Biborka Dániel, Borsos Balázs, Fehérvári Donát, Fekete Patrik, Győrffy Nándor, Han Ziying, Horváth Milán, Jójárt Emese, Josepovits Gábor, Kiss 625 Dóra, Kovács Benedek Noel, Kurucz Márton, Lőw László, Mészáros Anna Veronika, Morvai Eliza, Murai Dóra Eszter, Nagy 123 Krisztina, Németh Dávid László, Németh Máté, Petrányi Lilla, Schleier Anna , Sipos Dorka, Szabó Réka, Szabó Viktória, Szakács Domonkos, Szekeres Laura Anna, Szirtes Hanna, Török Hanga, Tran Dávid, Várhegyi Hajnal Eszter, Viczián Dániel, Waldhauser Miklós. 4 pontot kapott: 22 versenyző. 3 pontot kapott: 29 versenyző. 2 pontot kapott: 27 versenyző. 1 pontot kapott: 24 versenyző. Nem versenyszerű: 5 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 4 dolgozat.
A KöMaL 2021. januári matematika feladatai

