 |
A C. 1645. feladat (2021. január) |
C. 1645. Egy hegyesszögű háromszögben – a szokásos jelöléseket használva – \(\displaystyle m_b\), \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) ebben a sorrendben egymás utáni pozitív egész számok. Mekkora a háromszög területe?
Javasolta: Tatár Zsuzsanna Mária (Esztergom)
(5 pont)
A beküldési határidő 2021. február 15-én LEJÁRT.
Megoldás. Az \(\displaystyle ABC\) háromszög hegyesszögű, ezért minden magassága a háromszögön belül van, így az \(\displaystyle m_b\) magasság is, az \(\displaystyle m_b\) magasság \(\displaystyle D\) talppontja pedig a \(\displaystyle CA\) oldal belső pontja. Tekintsük a következő ábrát.
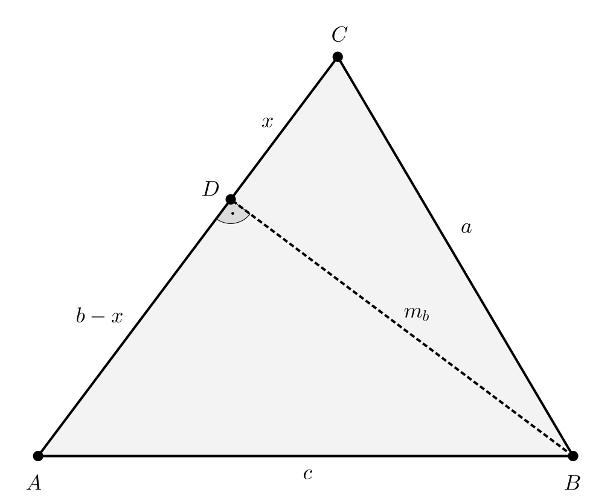
A feltétel szerint az \(\displaystyle m_b\), \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) ebben a sorrendben egymás utáni pozitív egész számok, ezért \(\displaystyle m_b=a-1\), \(\displaystyle b=a+1\) és \(\displaystyle c=a+2\).
Az ábra \(\displaystyle ABD\) és \(\displaystyle BCD\) derékszögű háromszögeire felírt Pitagorasz-tételekből azt kapjuk, hogy \(\displaystyle c^2-(b-x)^2=a^2-x^2\), azaz
\(\displaystyle (a+2)^2-((a+1)-x)^2=a^2-x^2.\)
Végezzzük el a műveleteket és rendezzük az egyenletet:
\(\displaystyle a^2+4a+4-(a^2+2a+1-2ax-2x+x^2)=a^2-x^2,\)
\(\displaystyle a^2-2a-3=2(a+1)x.\)
Az egyenlet bal oldala szorzattá alakítható:
\(\displaystyle (a+1)(a-3)=2(a+1)x,\)
amelyből a nyilván pozitív \(\displaystyle a+1\) tényezővel osztva azt kapjuk, hogy
| \(\displaystyle (1)\) | \(\displaystyle x=\frac{a-3}{2}.\) |
Az ábra \(\displaystyle BCD\) háromszögére felírhatjuk a Pitagorasz-tételt: \(\displaystyle x^2+(a-1)^2=a^2\), vagyis (1) alapján
\(\displaystyle \frac{(a-3)^2}{4}+(a-1)^2=a^2.\)
Végezzük el a műveleteket és rendezzük az egyenletet:
\(\displaystyle a^2-6a+9+(4a^2-8a+4)=4a^2,\)
| \(\displaystyle (2)\) | \(\displaystyle a^2-14a+13=0.\) |
A (2) másodfokú egyenlet gyökei: \(\displaystyle a_1=1\) és \(\displaystyle a_2=13\).
Az \(\displaystyle a_1=1\) nyilván nem megoldás, mert ebben az esetben az \(\displaystyle m_b\) magasság hossza \(\displaystyle 0\) lenne. Ezért csak az \(\displaystyle a_2=13\) megoldása a feladatnak. Ezt figyelembe véve \(\displaystyle m_b=12, a=13, b=14\) és \(\displaystyle c=15\).
A háromszög területe tehát (területegységben számolva):
\(\displaystyle T=\frac{b\cdot{m_b}}{2}=\frac{14\cdot12}{2}=84.\)
Statisztika:
116 dolgozat érkezett. 5 pontot kapott: 63 versenyző. 4 pontot kapott: 26 versenyző. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 4 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2021. januári matematika feladatai

