 |
A C. 1659. feladat (2021. március) |
C. 1659. Az \(\displaystyle AB\) szakasz \(\displaystyle A\) pontjából induló \(\displaystyle a\) félegyenes a szakasszal \(\displaystyle 0^\circ< \alpha<90^{\circ}\)-os, a \(\displaystyle B\)-ből induló \(\displaystyle b\) félegyenes pedig \(\displaystyle 0^\circ<\beta<90^{\circ}\)-os szöget zár be. A két félegyenes az \(\displaystyle AB\) egyenese által meghatározott két különböző félsíkban helyezkedik el. Az \(\displaystyle AB\) átmérőjű kör az \(\displaystyle a\)-t \(\displaystyle A_1\)-ben, a \(\displaystyle b\)-t pedig \(\displaystyle B_1\)-ben metszi másodszor. Az \(\displaystyle A_1B_1\) átmérőjű kör az \(\displaystyle a\)-ra illeszkedő egyenest \(\displaystyle A_2\)-ben, a \(\displaystyle b\)-re illeszkedő egyenest pedig \(\displaystyle B_2\)-ben metszi másodszor. Milyen összefüggés van \(\displaystyle \alpha\) és \(\displaystyle \beta\) között, ha \(\displaystyle A_1B_1\) és \(\displaystyle A_2B_2\) merőlegesek?
(5 pont)
A beküldési határidő 2021. április 12-én LEJÁRT.
Megoldás. Tekintsük a következő ábrát, amelyen az \(\displaystyle AB\) átmérőjű \(\displaystyle C\) középpontú kört \(\displaystyle k_1\)-gyel, az \(\displaystyle A_1B_1\) átmérőjű \(\displaystyle D\) középpontú kört \(\displaystyle k_2\)-vel jelöltük.
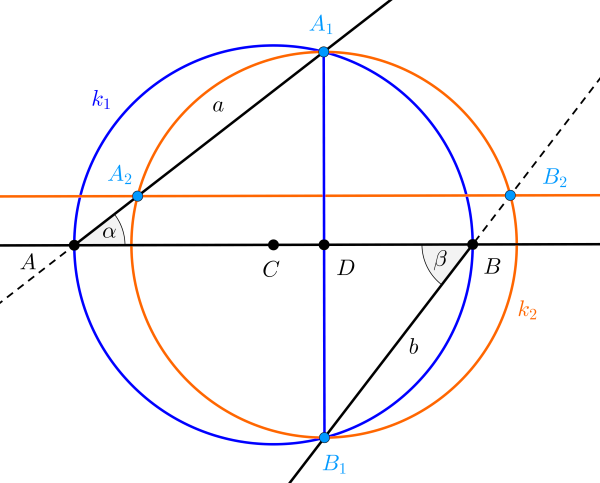
A \(\displaystyle k_1\) körben az \(\displaystyle A_1B\) húr az \(\displaystyle A\) pontból \(\displaystyle \alpha\) szög alatt látszik, ennek a húrnak a \(\displaystyle B_1\) pontból mért látószöge a kerületi szögek tétele szerint ugyancsak \(\displaystyle \alpha\). Ebből az is következik, hogy \(\displaystyle B_2B_1A_1\sphericalangle=\alpha\) is igaz, de akkor a \(\displaystyle k_2\) körben a kerületi szögek tétele miatt fennáll, hogy
\(\displaystyle B_2A_2A_1\sphericalangle=\alpha.\)
Ez azt jelenti, hogy a \(\displaystyle B_2A_2A_1\sphericalangle\) és \(\displaystyle BAA_1\sphericalangle\) egyenlő nagyságú szögek, melyeknek egyik szára ugyanazon az egyenesen van, ezért a másik két száruknak párhuzamosnak kell lenni, azaz
| \(\displaystyle (1)\) | \(\displaystyle AB\parallel{A_2B_2}.\) |
Ezért, ha a feltétel alapján \(\displaystyle A_1B_1\) merőleges \(\displaystyle A_2B_2\)-re, akkor (1) szerint \(\displaystyle A_1B_1\perp{AB}\) is igaz.
Az \(\displaystyle A_1B_1\) szakasz tehát a \(\displaystyle k_1\) körnek az \(\displaystyle AB\) átmérőre merőleges húrja, ezért az \(\displaystyle A_1B_1\) szakasz \(\displaystyle D\) felezőpontja az \(\displaystyle AB\) egyenesen van. Ebből következik, hogy a \(\displaystyle B_1BD\) olyan derékszögű háromszög, amelyben egyrészt \(\displaystyle B_1BD\sphericalangle=\beta\), másrészt \(\displaystyle B_2B_1A_1\sphericalangle=\alpha\) alapján \(\displaystyle BB_1D\sphericalangle=\alpha\) teljesül, azaz
\(\displaystyle \alpha+\beta=90^{\circ}.\)
Tehát ha a feladatban megadott feltételek mellett \(\displaystyle A_1B_1\perp{A_2B_2}\), akkor az \(\displaystyle \alpha\) és \(\displaystyle \beta\) szögek összege egy derékszöggel egyenlő.
Megjegyzések.
1) Ha \(\displaystyle \alpha\) és \(\displaystyle \beta\) a feltételnek megfelelő hegyesszögek, akkor a feladatban szereplő \(\displaystyle A_1, B_1, A_2, B_2\) pontok mindegyike létrejön.
2) A feladat feltételei akkor is teljesülnek, ha \(\displaystyle \alpha=\beta=45^{\circ}\). Ekkor az \(\displaystyle A_1\) és \(\displaystyle B_1\) pontok létrejönnek, és mivel az \(\displaystyle ABA_1\) és \(\displaystyle ABB_1\) egyenlő szárú derékszögű háromszögek, ezért \(\displaystyle A_1B_1\) merőlegesen felezi \(\displaystyle AB\)-t, vagyis a \(\displaystyle C, D\) pontok azonosak, tehát a \(\displaystyle k_1, k_2\) körök is egybeesnek. Ennek az a következménye, hogy az \(\displaystyle A_2, B_2\) pontok is létrejönnek, mégpedig úgy, hogy \(\displaystyle A=A_2\) és \(\displaystyle B=B_2\), azaz valóban fennáll a feladat \(\displaystyle A_1B_1\perp{A_2B_2}\) feltétele. Ekkor nyilvánvaló, hogy a teljesül megoldásban kapott \(\displaystyle \alpha+\beta=90^{\circ}\) összefüggés is.
Statisztika:
A KöMaL 2021. márciusi matematika feladatai
