 |
A C. 1678. feladat (2021. május) |
C. 1678. Egy négyoldalú szabályos gúla minden éle \(\displaystyle a\) hosszúságú. Kössük össze a gúla lapjainak középpontjait minden lehetséges módon. Bizonyítsuk be, hogy az így keletkezett szakaszok közül bármelyik hármat kiválasztva a szakaszokból lehet háromszöget szerkeszteni.
(5 pont)
A beküldési határidő 2021. június 10-én LEJÁRT.
Megoldás. A gúla alaplapja az \(\displaystyle a\) oldalú \(\displaystyle ABCD\) négyzet, oldallapjai az \(\displaystyle ABE, BCE, CDE\) és \(\displaystyle DAE\) szabályos háromszögek, a megfelelő lapközéppontok legyenek rendre \(\displaystyle O, P, Q, R\) és \(\displaystyle S\). Tekintsük a feltételeknek megfelelően készített ábrát.
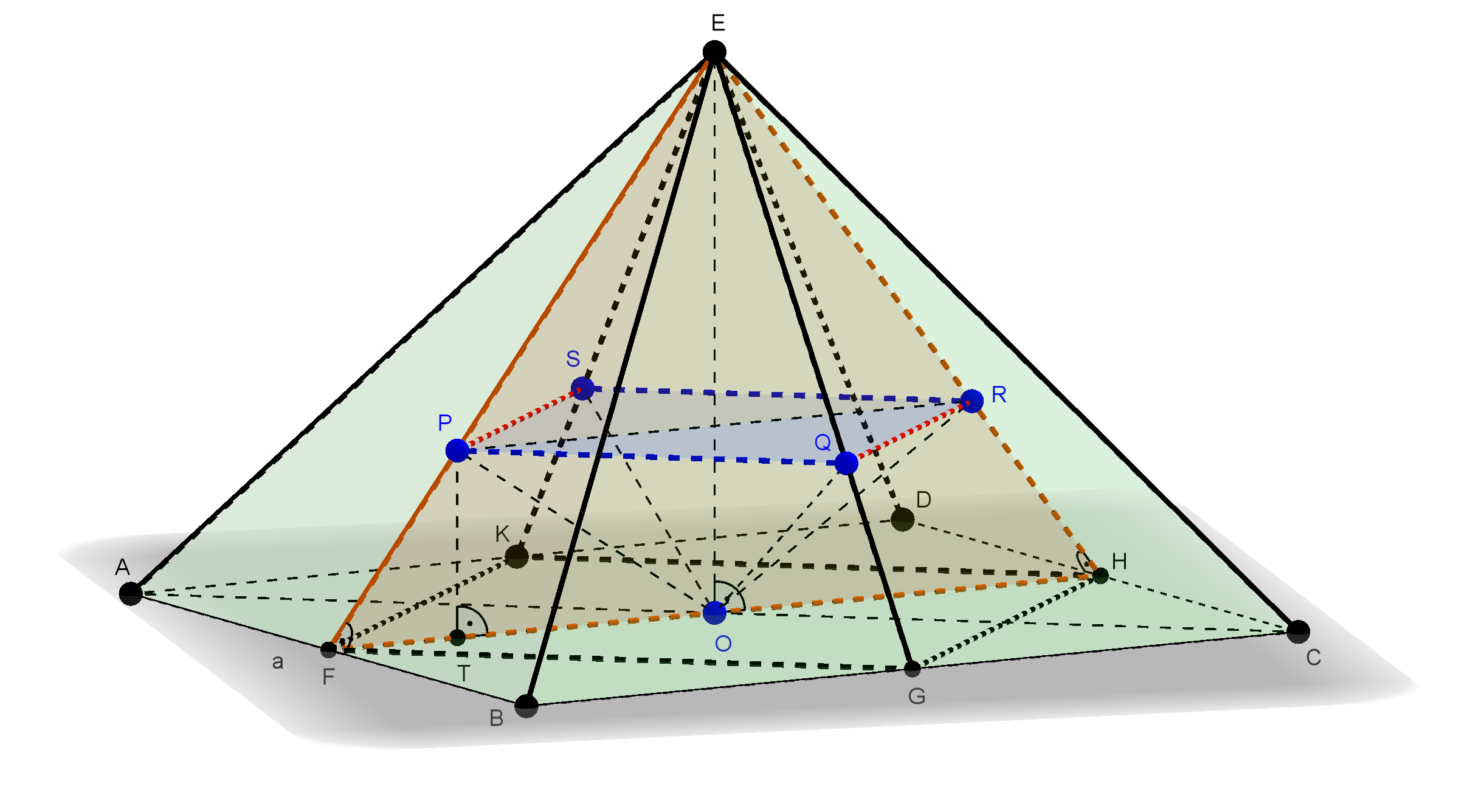
Az ábrán az \(\displaystyle AB, BC, CD\) és \(\displaystyle DA\) élek felezőpontjai rendre \(\displaystyle F, G,H\) és \(\displaystyle K\).
Nyilvánvaló, hogy a \(\displaystyle P, Q, R, S\) pontok a megfelelő háromszöglapok súlypontjai. Így az \(\displaystyle EF\) és \(\displaystyle EH\) szakaszok az egybevágó \(\displaystyle ABE\) és \(\displaystyle CDE\) szabályos háromszögek súlyvonalai, tehát egyrészt \(\displaystyle EF=EH\), másrészt a \(\displaystyle P, R\) súlypontok tulajdonsága miatt
\(\displaystyle \frac{EP}{EF}=\frac{ER}{EH}=\frac{2}{3},\)
ezért a párhuzamos szelők tételének megfordítása alapján \(\displaystyle PR\parallel{FH}\).
A párhuzamos szelőszakaszok tétele szerint:
\(\displaystyle \frac{PR}{FH}=\frac{EP}{EF}=\frac{2}{3},\)
ebből \(\displaystyle FH=a\) alapján
| \(\displaystyle (1)\) | \(\displaystyle PR=\frac{2a}{3}=\frac{4a}{6}\) |
következik.
Hasonlóképpen láthatjuk be, hogy \(\displaystyle SQ=\frac{4a}{6}\) is igaz.
Az \(\displaystyle EFG\) egyenlő szárú háromszög szárait metsző \(\displaystyle PQ\) és \(\displaystyle FG\) egyenesekre is alkalmazhatjuk a szelőszakaszok tételét:
\(\displaystyle \frac{PQ}{FG}=\frac{EP}{EF}=\frac{2}{3},\)
és mivel \(\displaystyle FG=\frac{AC}{2}=\frac{a\cdot{\sqrt{2}}}{2}\), ezért
| \(\displaystyle (2)\) | \(\displaystyle PQ=\frac{2a\cdot{\sqrt{2}}}{6}.\) |
Ugyanígy mutathatjuk meg, hogy \(\displaystyle QR=RS=SP=\frac{2a\cdot{\sqrt{2}}}{6}\) is teljesül.
Most már csak a gúla szimmetriája miatt egyenlő hosszúságú \(\displaystyle OP, OQ, OR, OS\) szakaszok hosszát kell meghatároznunk. Ehhez az ábrán a \(\displaystyle P\) pontból merőlegest állítottunk az \(\displaystyle ABCD\) négyzet síkjára, a merőleges \(\displaystyle T\) talppontja a négyzet \(\displaystyle FH\) középvonalára illeszkedik, ugyanezen a szakaszon van a gúla \(\displaystyle EO\) magasságának \(\displaystyle O\) talppontja, és világos, hogy a \(\displaystyle PT\) és \(\displaystyle EO\) szakaszok is az \(\displaystyle EFH\) háromszög síkjában vannak, ezért \(\displaystyle PT\parallel{EO}\).
Az \(\displaystyle EFO\) derékszögű háromszögre felírva a Pitagorasz-tételt:
\(\displaystyle {\Bigg(\frac{a}{2}\Bigg)}^2+{EO}^2={\Bigg(\frac{a\cdot{\sqrt{3}}}{2}\Bigg)}^2,\)
ahonnan \(\displaystyle EO=\frac{a\cdot{\sqrt{2}}}{2}\).
A párhuzamos szelőszakaszok tételét alkalmazva kapjuk, hogy \(\displaystyle PT=\frac{EO}{3}=\frac{a\cdot{\sqrt{2}}}{6}\), továbbá \(\displaystyle FT=\frac{FO}{3}=\frac{a}{6}\) és ezért \(\displaystyle TO=\frac{2a}{6}\).
Az \(\displaystyle OPT\) derékszögű háromszögre felírjuk a Pitagorasz-tételt: \(\displaystyle {OP}^2={TO}^2+{PT}^2\), azaz
\(\displaystyle {OP}^2={\Bigg(\frac{2a}{6}\Bigg)}^2+{\Bigg(\frac{a\cdot{\sqrt{2}}}{6}\Bigg)}^2,\)
ebből egyszerű számolással adódik:
| \(\displaystyle (3)\) | \(\displaystyle OP=\frac{a\cdot{\sqrt{6}}}{6}.\) |
Ugyanilyen hosszúságúak az \(\displaystyle OQ, OR, OS\) szakaszok is.
Számításaink szerint tehát a gúla lapközéppontjait összekötő szakaszok között háromféle hosszúság fordul elő, mégpedig az (1)-nek megfelelő hosszúságú \(\displaystyle PR\) és \(\displaystyle SQ\) szakaszok, a (2)-nek mmegfelelő \(\displaystyle PQ, QR, RS\) és \(\displaystyle SP\) szakaszok, végül a (3)-nak eleget tevő \(\displaystyle OP, OQ, OR\) és \(\displaystyle OS\) szakaszok.
A feladat állítása szerint ezen tíz szakasz közül bármely hármat kiválasztva, a kapott szakaszokból lehet háromszöget szerkeszteni, azaz érvényes rájuk a háromszög-egyenlőtlenség.
Ha három egyforma hosszúságú szakaszt választunk ki (ez csak a \(\displaystyle PQ, QR, RS, SP\) vagy az \(\displaystyle OP, OQ, OR, OS\) szakaszok esetén lehetséges), azokra nyilván teljesül a háromszög-egyenlőtlenség. Ha a három kiválasztott szakasz mind különböző hosszúságú, akkor elegendő ellenőrizni a háromszög-egyenlőtlenséget (1)-(2)-(3) alapján a \(\displaystyle 4; 2\cdot{\sqrt{2}}\) és \(\displaystyle \sqrt{6}\) számokra. Ezekre viszont biztosan teljesül, hogy a két legkisebb szám összege nagyobb, mint a legnagyobb szám, azaz:
\(\displaystyle 2\cdot{\sqrt{2}}+\sqrt{6}>4.\)
Ez egyszerűen belátható, hiszen a bal oldal mindkét gyökös kifejezése nagyobb 2-nél. Ha a három kiválasztott szakasz között van két egyforma, akkor elegendő vizsgálni a következő számhármasokat:
\(\displaystyle 4, 4, 2\cdot{\sqrt{2}};\qquad{4, 4, \sqrt{6}},\)
\(\displaystyle 2\cdot{\sqrt{2}}, 2\cdot{\sqrt{2}}, 4;\qquad{2\cdot{\sqrt{2}}, 2\cdot{\sqrt{2}},\sqrt{6}},\)
és
\(\displaystyle \sqrt{6}, \sqrt{6}, 4; \qquad{\sqrt{6}, \sqrt{6},2\cdot{\sqrt{2}}}.\)
Az előző esethez hasonlóan könnyen igazolható, hogy mindezen a számhármasokra teljesül, hogy bármely két szám összege nagyobb a harmadiknál.
Ez pedig azt jelenti, hogy a háromszög-egyenlőtlenség akkor is fennáll, ha a három kiválasztott szakasz között van két egyforma.
Ezzel a feladat megoldását befejeztük.
Megjegyzés. Bizonyítható, hogy \(\displaystyle OP\) merőleges a gúla \(\displaystyle ABE\) lapjára, ennek alapján az \(\displaystyle OP\) szakasz az \(\displaystyle OPE\) derékszögű háromszögből is kiszámítható.
Statisztika:
19 dolgozat érkezett. 5 pontot kapott: Andó Lujza, Biró 424 Ádám, Dobi Dorina Lili, Molnár Réka, Németh László Csaba, Xu Yiling. 4 pontot kapott: Féger Tamás, Horváth 828 Mátyás, Kadem Aziz, Németh Máté Előd, Schneider Anna, Szalanics Tamás, Téglás Panna, Zaránd Andris. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2021. májusi matematika feladatai

