Problem C. 1692. (November 2021)

C. 1692. \(\displaystyle P\) is an interior point of side \(\displaystyle DA\) of a square \(\displaystyle ABCD\). The angle bisector of \(\displaystyle \angle PBC\) intersects side \(\displaystyle CD\) at point \(\displaystyle Q\), and the foot of the perpendicular dropped from point \(\displaystyle Q\) to line \(\displaystyle BP\) is \(\displaystyle R\). Find the angle of the lines \(\displaystyle AR\) and \(\displaystyle BQ\).

(5 pont)

Deadline expired on December 10, 2021.

Sorry, the solution is available only in Hungarian. Google translation

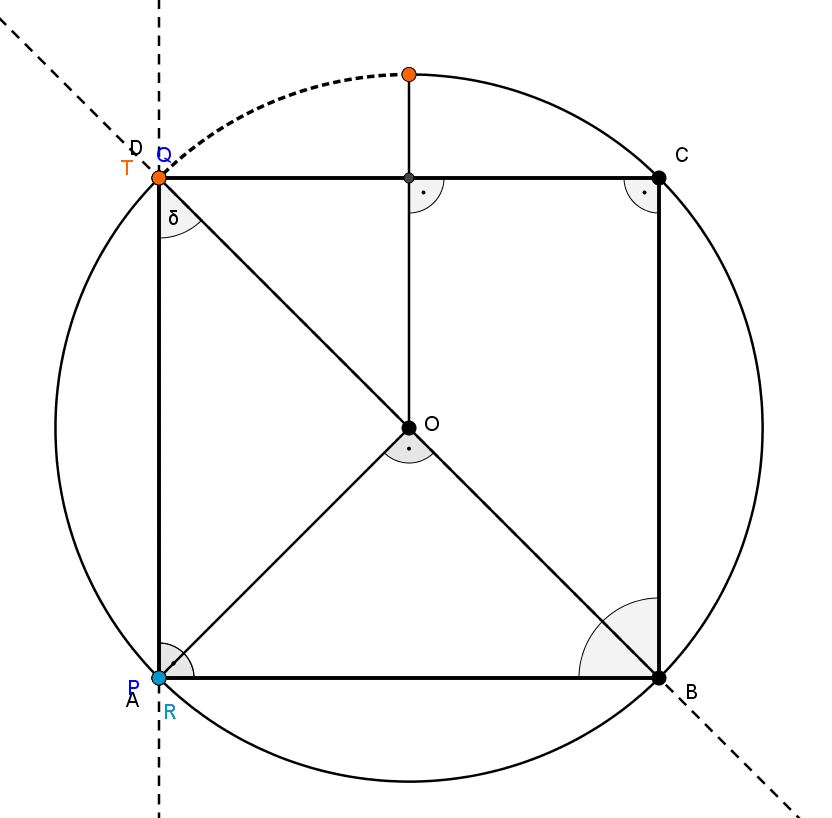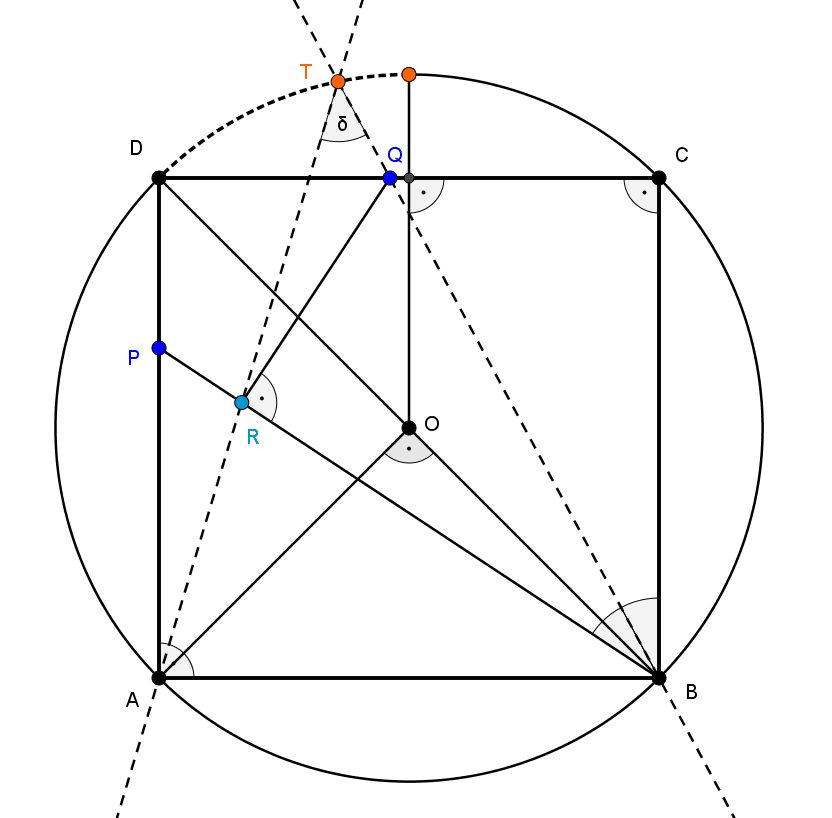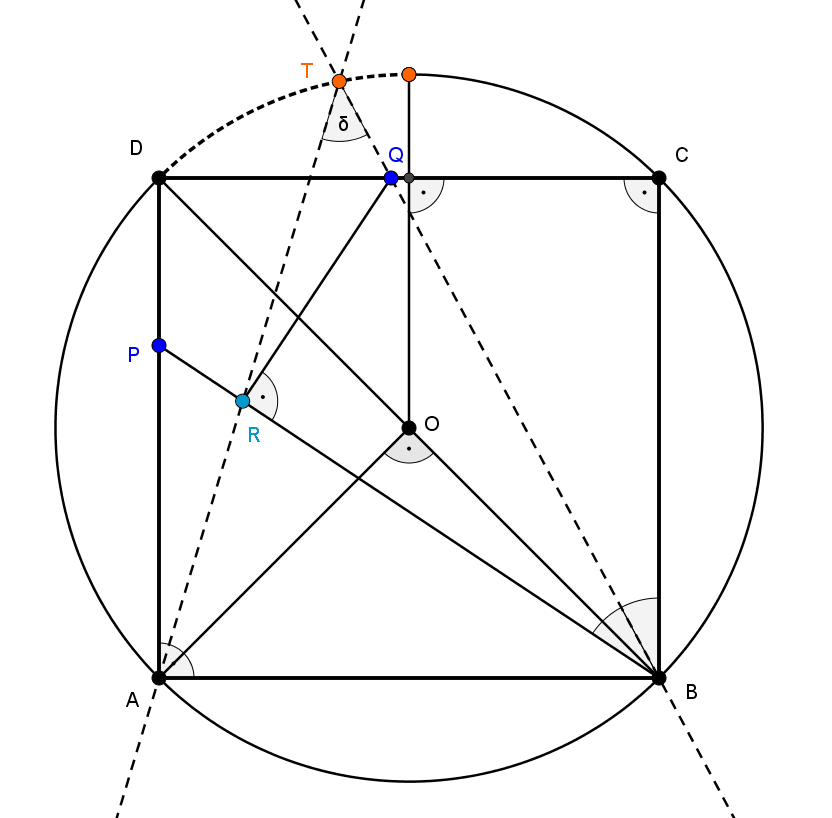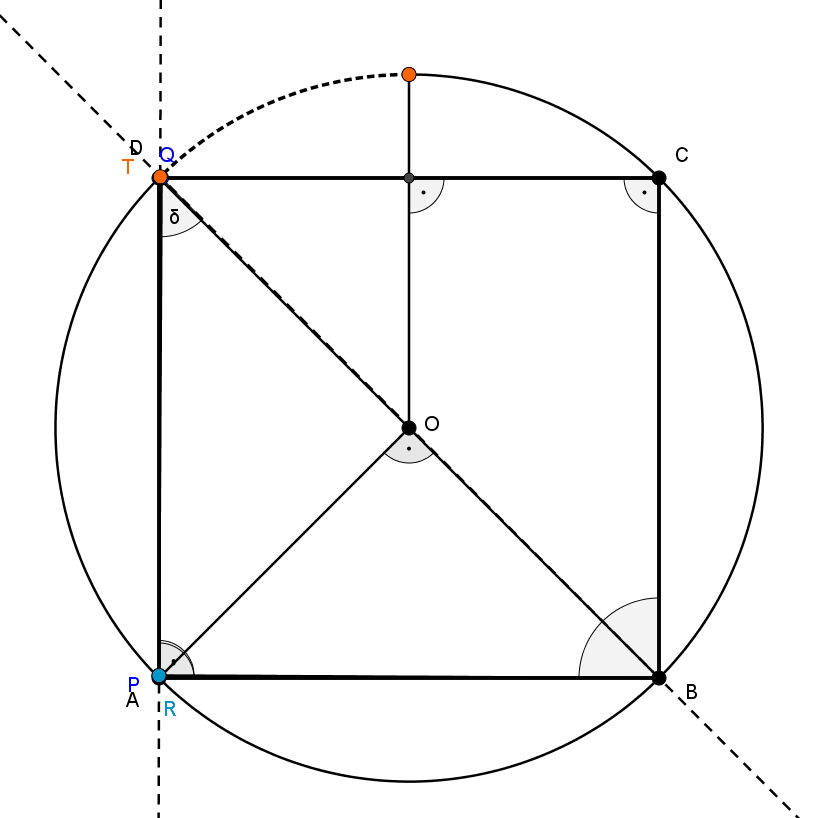
Megoldás. Jelöléseink az alábbi ábrán láthatók, ezen a \(\displaystyle QR\) egyenes a \(\displaystyle DA\) szakaszt az \(\displaystyle S\) pontban metszi, az \(\displaystyle AR\) és \(\displaystyle BQ\) egyenesek metszéspontja \(\displaystyle T\). A kerületi-középponti szögekről lásd a Középponti szögek, kerületi szögek, látószögkörív című cikket a https://www.komal.hu/cikkek/cikklista.h.shtml oldalon.

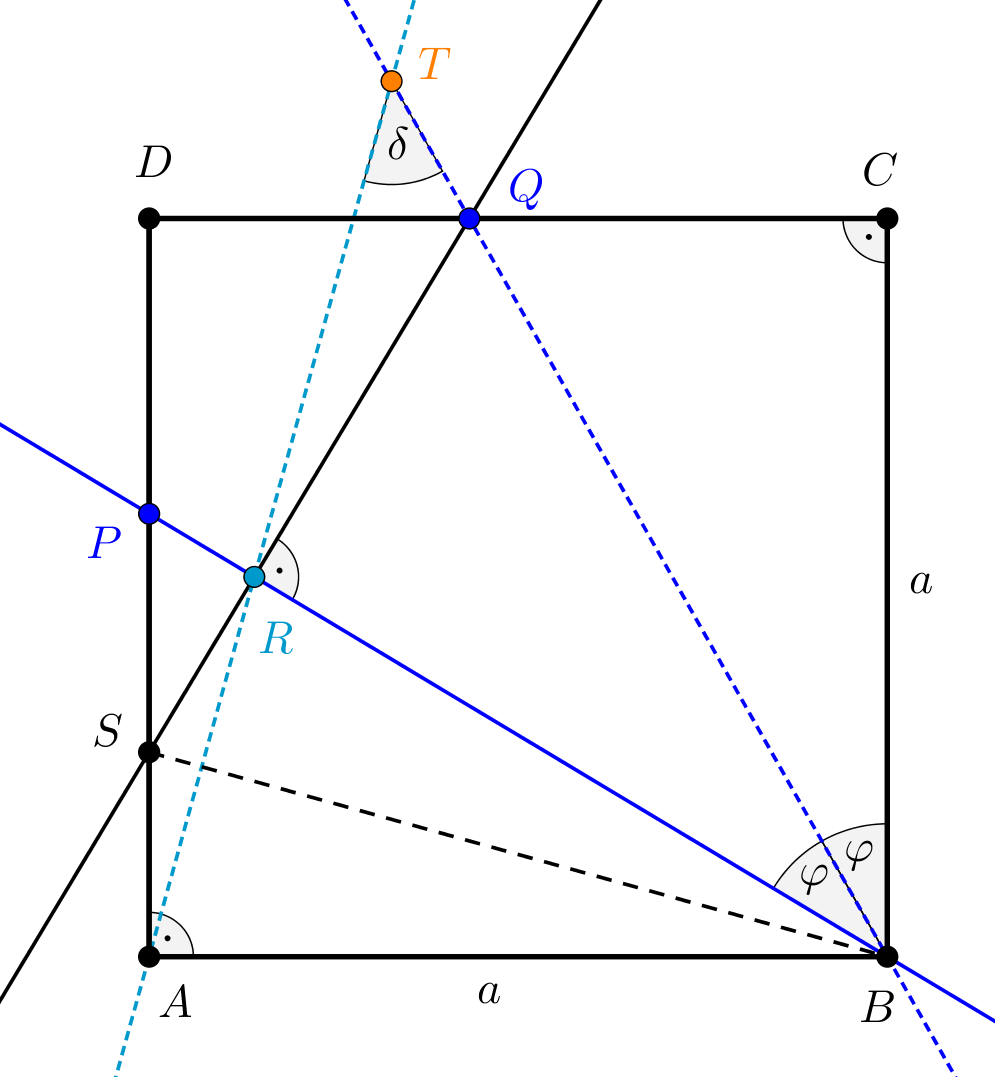
A \(\displaystyle PBC\sphericalangle=2\varphi\) szöget felező \(\displaystyle BQ\) egyenes minden pontjára, így a \(\displaystyle B\) pontra is igaz, hogy a pontból a szárakra bocsátott merőlegesek a szárakból egyenlő hosszúságú szakaszokat vágnak le, ezért \(\displaystyle BC=BR=a\). A \(\displaystyle BAS\) és \(\displaystyle BRS\) derékszögű háromszögekben egy-egy befogó hossza egyenlő, hiszen \(\displaystyle BR=BA=a\), a \(\displaystyle BS\) átfogó pedig közös, a \(\displaystyle BAS\) és \(\displaystyle BRS\) derékszögű háromszögek ezért egybevágók. Ez azt is jelenti, hogy a \(\displaystyle BS\) egyenes felezi az \(\displaystyle ABR\sphericalangle=90^{\circ}-2\varphi\) szöget, azaz

Az \(\displaystyle ABRS\) négyszög csúcsai a \(\displaystyle BS\) szakasz mint átmérő fölé írt Thalész-körre illeszkednek, így a négyszög amellett, hogy deltoid, húrnégyszög is. Ebből a tulajdonságából az következik, hogy a köré írt körben az \(\displaystyle ABS\sphericalangle\) és \(\displaystyle ARS\sphericalangle\) azonos ívhez tartozó kerületi szögek, tehát egyenlő nagyságúak, ezért (1) felhasználásával \(\displaystyle ARS\sphericalangle=45^{\circ}-\varphi\).

Ugyanakkor \(\displaystyle ARS\sphericalangle\) és \(\displaystyle TRQ\sphericalangle\) csúcsszögek és ezért egyenlő nagyságúak, vagyis \(\displaystyle TRQ\sphericalangle=45^{\circ}-\varphi\).

A \(\displaystyle BTR\) háromszögben a szögek összege \(\displaystyle \varphi+\delta+90^{\circ}+TRQ\sphericalangle=180^{\circ}\), azaz

\(\displaystyle \varphi+\delta+90^{\circ}+45^{\circ}-\varphi=180^{\circ},\)

ahonnan egyszerű számolással kapjuk, hogy \(\displaystyle \delta=45^{\circ}\). Eszerint a \(\displaystyle DA\) oldal bármely belső \(\displaystyle P\) pontjából indulunk ki, az \(\displaystyle AR\) és \(\displaystyle BQ\) egyenesek \(\displaystyle 45^{\circ}\)-os szögben metszik egymást.

Az alábbi ábrán (animáción) \(\displaystyle P\) befutja az \(\displaystyle AB\) szakaszt:

Megjegyzés. Ha megengedjük, hogy a \(\displaystyle P\) pont a \(\displaystyle DA\) szakasz valamelyik végpontjával azonos legyen, akkor \(\displaystyle P=A\) esetén \(\displaystyle Q=D\) valósul meg és így \(\displaystyle R=A\) is igaz. Ekkor azonban az \(\displaystyle AR\) egyenes nem jön létre, hiszen az \(\displaystyle A\) és \(\displaystyle R\) pontok azonosak. Ha ebben az esetben az \(\displaystyle AR\) egyenesnek a \(\displaystyle DA\) egyenest tekintenénk, akkor \(\displaystyle AR\) és \(\displaystyle BQ\) ismét \(\displaystyle 45^{\circ}\)-os szöget zárna be.

A \(\displaystyle P=D\) esetben egyrészt az \(\displaystyle S\) pont a \(\displaystyle DA\) szakasz felezőpontja lenne, továbbá \(\displaystyle \varphi=22,5^{\circ}\) valósulna meg, az \(\displaystyle AR\) és \(\displaystyle BQ\) egyenesek pedig ezúttal is \(\displaystyle 45^{\circ}\)-os szöget zárnának be.

Statistics:

38 students sent a solution.
5 points:	Baksai Bálint, Besze Zsolt, Cynolter Dorottya, Deák Gergely, Egyházi Hanna, Fekete Patrik, Hajós Balázs, Halász Henrik, Horváth 328 Áron, Horváth Milán, Hosszu Noel, Keszthelyi Eszter, Kiss 625 Dóra, Nagy Daniella, Németh Máté Előd, Pekk Márton, Radzik Réka, Rumpler Bianka, Schneider Dávid, Sipeki Márton, Szabó Zóra, Szalanics Tamás, Tóth Gréta, Waldhauser Miklós, Werner Kinga.
4 points:	Biborka Dániel, Magyar Gábor Balázs, Szabó Réka, Szamkó Szabolcs, Szittyai Anna, Váczy Dorottya.
3 points:	3 students.
2 points:	2 students.

Problems in Mathematics of KöMaL, November 2021