A C. 1702. feladat (2022. január)

C. 1702. Az $\displaystyle ABCD$ négyszög $\displaystyle A$ csúcsa illeszkedik az $\displaystyle S$ síkra, $\displaystyle BD$ átlója párhuzamos a síkkal, $\displaystyle C$ csúcsa $\displaystyle 8$ egység távolságra van az $\displaystyle S$ síktól. Azt tapasztaljuk, hogy a négyszög $\displaystyle S$-re vonatkozó merőleges vetülete egy négyzet, melynek átlója $\displaystyle 6$ egység. Bizonyítsuk be, hogy az $\displaystyle ABCD$ négyszög rombusz, valamint számítsuk ki az oldalainak hosszát.

Javasolta: Zagyva Tiborné (Baja)

(5 pont)

A beküldési határidő 2022. február 10-én LEJÁRT.

Megoldás. Jelölje az $\displaystyle ABCD$ négyszög csúcsainak az $\displaystyle S$ síkra eső merőleges vetületeit rendre $\displaystyle A', B', C', D'$. A feltétel miatt egyrészt $\displaystyle A'\equiv{A}$, illetve $\displaystyle A'B'C'D'$ négyzet, másrészt $\displaystyle CC'=8$, valamint $\displaystyle A'C'=B'D'=6$. Az $\displaystyle ABCD$ négyszögben $\displaystyle O$-val jelöltük azt a pontot, amelynek merőleges vetülete az $\displaystyle S$ síkon az $\displaystyle A'B'C'D'$ négyzet $\displaystyle O'$ középpontja.

Tekintsük a következő ábrát.

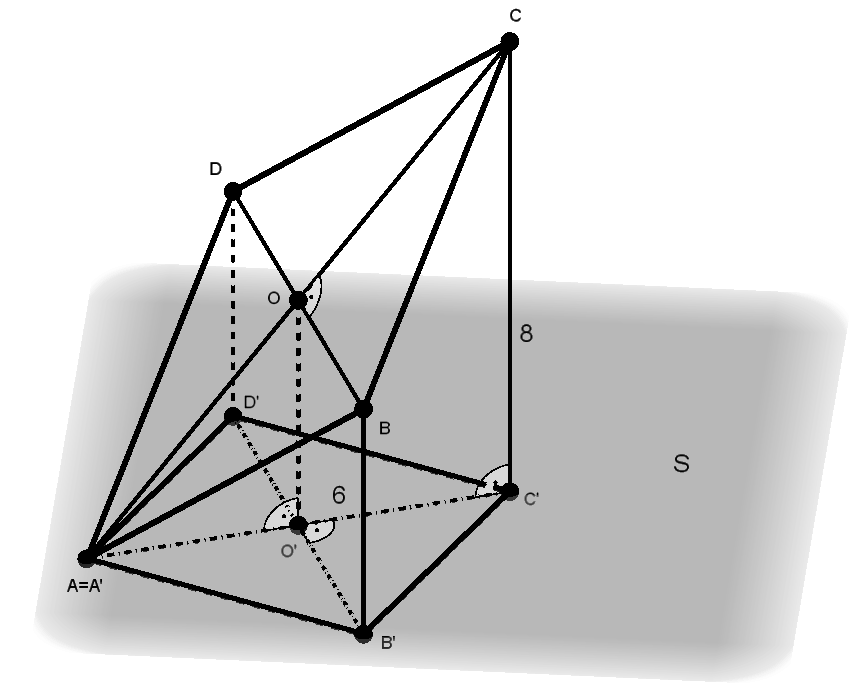
Ha két egyenes merőleges egymásra és az egyik párhuzamos az $\displaystyle S$ síkkal, akkor az egyenesek vetülete is merőleges egymásra, és ez megfordítva is igaz. Ez a feltétel miatt fennáll, hiszen $\displaystyle A'C'\perp{B'D'}$, ezért $\displaystyle AC\perp{BD}$ is teljesül. A merőleges vetítés illeszkedéstartó, így, mivel $\displaystyle A'C'\cap{B'D'}=O'$, ezért $\displaystyle AC\cap{BD}=O$ is érvényes.

Ugyanakkor $\displaystyle O'$ felezi a $\displaystyle B'D'$ szakaszt, tehát $\displaystyle O$ felezi a $\displaystyle BD$ szakaszt.

Az $\displaystyle AC'C$ háromszögben $\displaystyle O'O$ középvonal, mert $\displaystyle O'$ felezi az $\displaystyle A'C'$ szakaszt is és $\displaystyle OO'\parallel{CC'}$. Ez azt jelenti, hogy $\displaystyle O$ felezi az $\displaystyle AC$ szakaszt is.

Eszerint az $\displaystyle ABCD$ négyszögben az $\displaystyle AC$ és $\displaystyle BD$ átlók merőlegesen felezik egymást, ezért az $\displaystyle ABCD$ négyszög rombusz.

$\displaystyle BD$ párhuzamos az $\displaystyle S$ síkkal és $\displaystyle B'D'=6$, ezért $\displaystyle BD=6$ is igaz, és akkor az előzőek szerint $\displaystyle BO=DO=3$.

A $\displaystyle 6$ és $\displaystyle 8$ befogójú $\displaystyle AC'C$ derékszögű háromszögből pedig a Pitagorasz-tétel felhasználásával azt kapjuk, hogy $\displaystyle AC=10$, és ezért $\displaystyle AO=CO=5$.

Az $\displaystyle O$ pontban derékszögű $\displaystyle AOB$ háromszögből a Pitagorasz-tétel alapján adódik, hogy $\displaystyle AB=\sqrt{5^2+3^2}=\sqrt{34}$. Az $\displaystyle ABCD$ rombusz oldalainak hossza tehát $\displaystyle AB=BC=CD=DA=\sqrt{34}$.

Statisztika:

36 dolgozat érkezett.
5 pontot kapott:	Besze Zsolt, Egyházi Hanna, Hajós Balázs, Horváth Milán, Hosszu Noel, Hugli Benedek, Josepovits Gábor, Keszthelyi Eszter, Kurucz Márton, Mészáros Anna Veronika, Murai Dóra Eszter, Nagy Daniella, Pekk Márton, Radzik Réka, Sipeki Márton, Süveges Gergő, Szabó Enikő Lilla, Szabó Réka, Szabó Zóra, Tóth Gréta, Werner Kinga, Xu Yiling.
4 pontot kapott:	Deák Gergely.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2022. januári matematika feladatai