 |
A C. 1705. feladat (2022. február) |
C. 1705. Egy deltoidról tudjuk, hogy húrnégyszög, oldalainak hossza 42 és 56 hosszúságegység. Milyen messze van egymástól a beírt és a köréírt körének középpontja?
Javasolta: Siposs András (Budapest)
(5 pont)
A beküldési határidő 2022. március 10-én LEJÁRT.
1. megoldás. A deltoid érintőnégyszög, mert a szemben levő oldalainak összege a tengelyes szimmetria miatt egyenlő. Ezért, ha a deltoid húrnégyszög is, akkor, mivel két szemben levő szöge egyenlő nagyságú, ezért ezek a szögek derékszögek. Legyen az \(\displaystyle ABCD\) deltoid szimmetriatengelye az \(\displaystyle AC\) átló, így a \(\displaystyle B\) és \(\displaystyle D\) csúcsoknál levő belső szögek \(\displaystyle 90^{\circ}\)-osak. Tekintsük a következő ábrát.
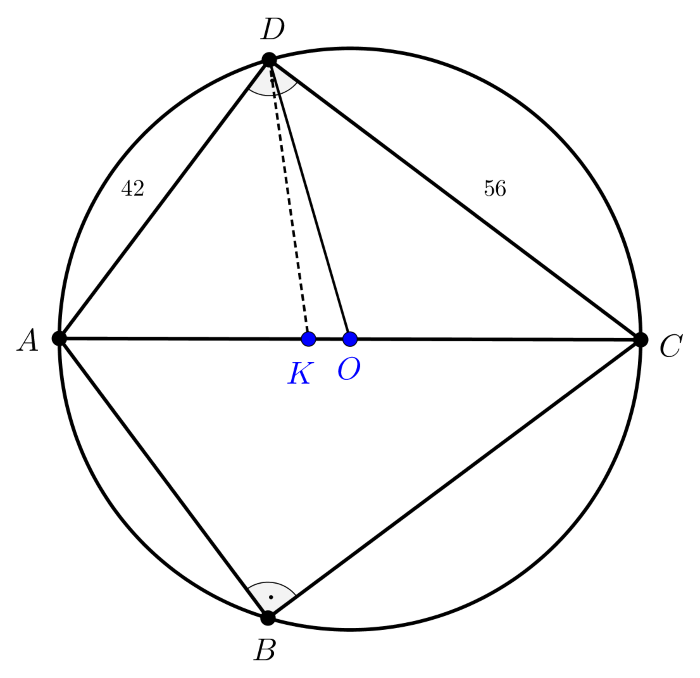
Az \(\displaystyle ABC\) és \(\displaystyle ADC\) derékszögű háromszögek, amelyeknek befogói a feltételek szerint \(\displaystyle AB=AD=42\) és \(\displaystyle BC=DC=56\).
A Pitagorasz-tételt alkalmazva \(\displaystyle 42^2+56^2={AC}^2\), ahonnan azt kapjuk, hogy \(\displaystyle AC=70\) hosszúságegység. A deltoid köré írt kör középpontja az \(\displaystyle AC\) átló \(\displaystyle O\) felezőpontja, így \(\displaystyle AO=35\).
Mivel a deltoid érintőnégyszög, ezért belső szögfelezői egy pontban metszik egymást. Az \(\displaystyle AC\) átló felezi az \(\displaystyle A\), illetve \(\displaystyle C\) csúcsnál levő belső szögeket, ezért a beírt kör középpontja az \(\displaystyle AC\) átlón van. Az ábrán megrajzoltuk a \(\displaystyle D\) csúcsnál levő derékszög szögfelezőjét, ez az átlót a beírt kör \(\displaystyle K\) középpontjában metszi.
Az \(\displaystyle ADC\) háromszögre felírjuk a belső szögfelező tételét:
\(\displaystyle \frac{AK}{70-AK}=\frac{42}{56},\)
innen egyszerű számolással kapjuk, hogy
\(\displaystyle 98AK=42\cdot70,\)
vagyis
\(\displaystyle AK=30.\)
Ebből azonnal következik \(\displaystyle AO=35\) alapján, hogy \(\displaystyle KO=5\), azaz a beírt és körülírt kör középpontja \(\displaystyle 5\) hosszúságegységre van egymástól.
2. megoldás. Felhasználjuk az 1. megoldás megállapításait és az ábra jelöléseit:
a \(\displaystyle B\) és \(\displaystyle D\) csúcsoknál levő belső szögek \(\displaystyle 90^{\circ}\)-osak, \(\displaystyle AC=70\), \(\displaystyle AO=35\), a beírt kör középpontja az \(\displaystyle AC\) átló \(\displaystyle K\) pontja.
Bocsássunk a \(\displaystyle K\) pontból merőlegeseket a \(\displaystyle CD\) és \(\displaystyle AD\) oldalakra, a merőlegesek talppontjai \(\displaystyle E\), illetve \(\displaystyle F\).
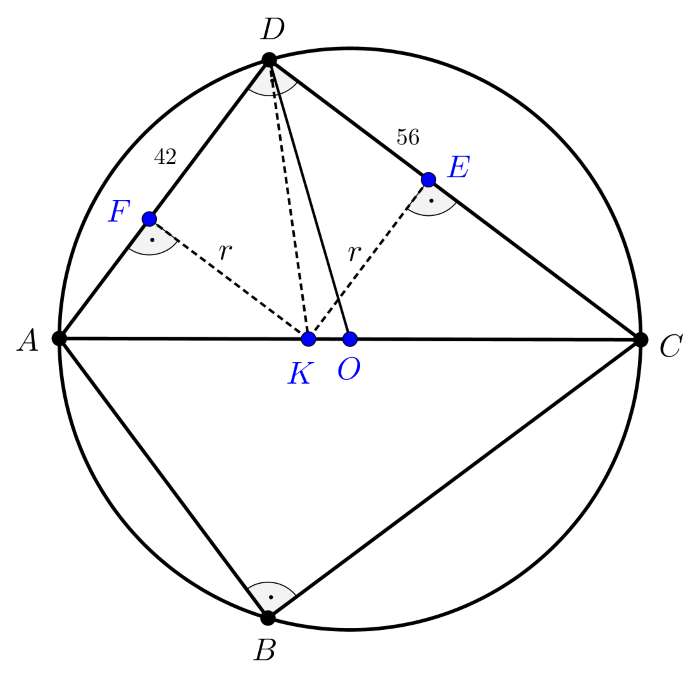
A \(\displaystyle KE\) és \(\displaystyle KF\) szakaszok hossza a beírt kör \(\displaystyle r\) sugara, a \(\displaystyle KEDF\) négyszög minden szöge derékszög, és \(\displaystyle KE=KF\) miatt a négyszög négyzet, tehát \(\displaystyle ED=FD=r\) is igaz.
Felhasználjuk azt a jól ismert összefüggést, hogy ha az \(\displaystyle ABCD\) érintőnégyszög területe \(\displaystyle t\), kerülete \(\displaystyle k\), akkor
| \(\displaystyle (1)\) | \(\displaystyle \frac{t}{k}=\frac{r}{2}.\) |
Az \(\displaystyle ABCD\) négyszög területe \(\displaystyle t=2\cdot{\frac{42\cdot56}{2}}=2352\) területegység, kerülete \(\displaystyle k=2\cdot(42+56)=196\) hosszúságegység, ennek megfelelően (1) alapján \(\displaystyle r=24\). Világos, hogy az \(\displaystyle AKF\) és \(\displaystyle ACD\) háromszögek hasonlók, hiszen megfelelő szögeik egyenlők az oldalak párhuzamossága, illetve egy egyenesre esése miatt.
A két háromszög megfelelő oldalainak aránya tehát egyenlő:
| \(\displaystyle (2)\) | \(\displaystyle \frac{r}{AK}=\frac{56}{AC}.\) |
Az \(\displaystyle r=24\) és \(\displaystyle AC=70\) behelyettesítése után (2)-ből adódik, hogy
\(\displaystyle AK=\frac{24\cdot70}{56}=30.\)
Ebből \(\displaystyle AO=35\) szerint következik, hogy \(\displaystyle KO=5\), ezért a beírt és körülírt kör középpontja \(\displaystyle 5\) hosszúságegységre van egymástól.
Megjegyzések. 1.) Az 1. megoldásban a szögfelezőtételből az is következik, hogy \(\displaystyle AK<CK\), tehát a \(\displaystyle K\) pont az ábrának megfelelően az \(\displaystyle AO\) szakasz belső pontja.
2.) Általánosan bizonyítható, hogy ha az \(\displaystyle ABCD\) deltoid húrnégyszög, szimmetriatengelye az \(\displaystyle AC\) átló, a négyszög oldalainak hossza \(\displaystyle a\) és \(\displaystyle b\), továbbá \(\displaystyle a<b\), akkor \(\displaystyle KO=\frac{((b-a)\sqrt{a^2+b^2}}{2(b+a)}\).
Ha \(\displaystyle b<a\), akkor az összefüggés számlálójában \(\displaystyle b-a\) helyett \(\displaystyle a-b\) szerepel, ha pedig \(\displaystyle a=b\), akkor a \(\displaystyle K\) és \(\displaystyle O\) pontok azonosak, vagyis \(\displaystyle KO=0\).
Statisztika:
138 dolgozat érkezett. 5 pontot kapott: 100 versenyző. 4 pontot kapott: 7 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 4 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2022. februári matematika feladatai
