Problem C. 1719. (April 2022)

C. 1719. In the interior of a regular triangle \(\displaystyle ABC\) consider the points \(\displaystyle P\) where side \(\displaystyle AB\) subtends an angle of \(\displaystyle 135^{\circ}\). Prove that the line segments \(\displaystyle PA\), \(\displaystyle PB\), \(\displaystyle PC\) can always form a triangle, and one angle of such triangles is always the same, independently of the position of point \(\displaystyle P\).

(5 pont)

Deadline expired on May 10, 2022.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A \(\displaystyle P\) pont az \(\displaystyle AB\) szakasz fölé, az \(\displaystyle ABC\) háromszög belsejébe rajzolt \(\displaystyle k\) látószögköríven helyezkedik el és nyilván nem esik egybe sem az \(\displaystyle A\), sem a \(\displaystyle B\) ponttal. (Lásd a látószögkörívvel is kapcsolatos rövid cikket honlapunkon.) A feltétel miatt ebből az következik, hogy \(\displaystyle BPA\sphericalangle=135^{\circ}\). Forgassuk el az \(\displaystyle A\) pont körül a \(\displaystyle PC\) szakaszt negatív irányba \(\displaystyle 60^{\circ}\)-kal. A \(\displaystyle C\) pont képe nyilván \(\displaystyle B\), a \(\displaystyle P\) pont képét \(\displaystyle P'\)-vel jelöltük.

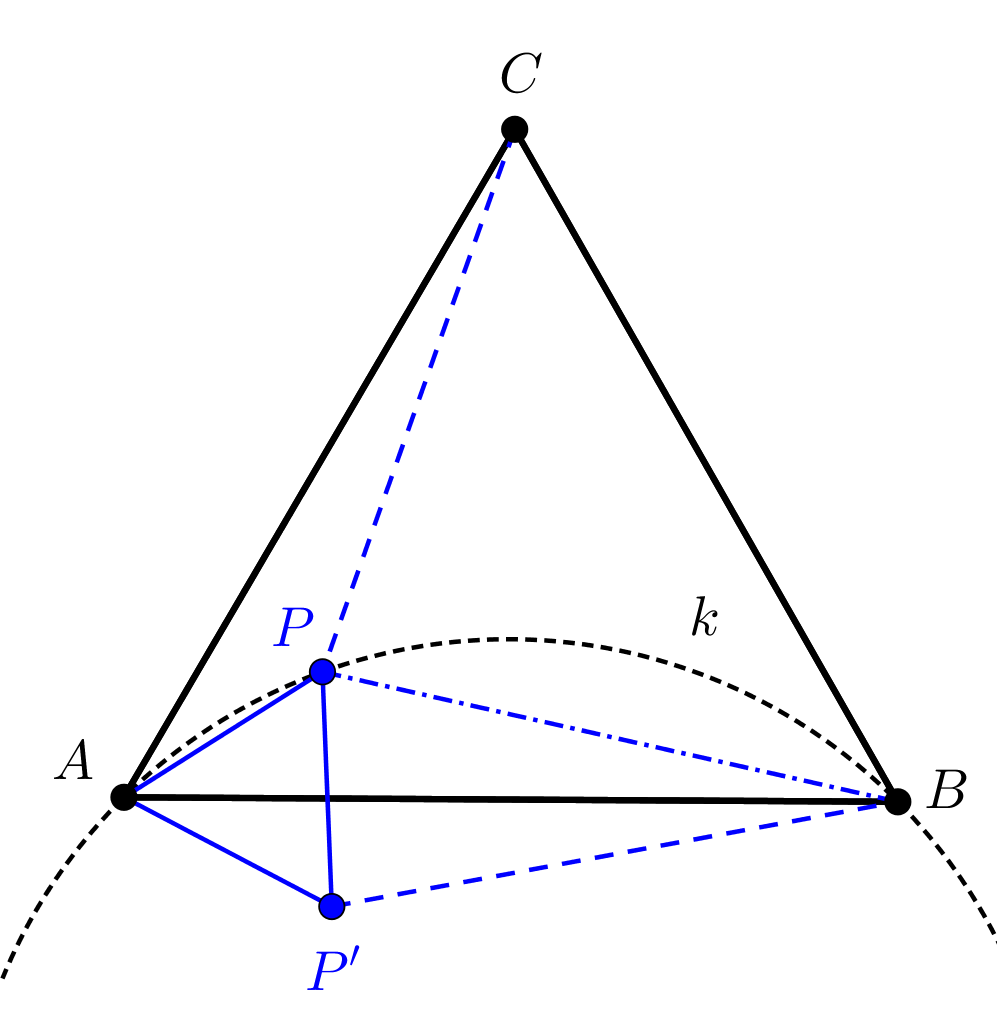
Az elforgatás tulajdonságai miatt egyrészt \(\displaystyle PC=P'B\), másrészt \(\displaystyle PA=P'A\), továbbá \(\displaystyle PAP'\sphericalangle=60^{\circ}\) miatt \(\displaystyle PAP'\) szabályos háromszög.

Ebből az következik, hogy \(\displaystyle PA=P'A=PP'\) is igaz.

A \(\displaystyle BPP'\) háromszög minden esetben létrejön és oldalaira teljesül, hogy \(\displaystyle PP'=PA\), illetve \(\displaystyle P'B=PC\). Így a \(\displaystyle PA, PB, PC\) szakaszokból a \(\displaystyle P\) pont bármely, a feltételnek megfelelő helyzete esetén valóban mindig lehet háromszöget szerkeszteni.

Mivel \(\displaystyle PAP'\) szabályos háromszög, ezért \(\displaystyle P'PA\sphericalangle=60^{\circ}\), ebből \(\displaystyle BPA\sphericalangle=135^{\circ}\) alapján \(\displaystyle BPP'\sphericalangle=75^{\circ}\) következik. Ezzel azt is igazoltuk, hogy a \(\displaystyle BPP'\) háromszög \(\displaystyle P\) csúcsánál levő belső szöge a \(\displaystyle P\) pont bármely helyzete esetén \(\displaystyle 75^{\circ}\)-os.

Megjegyzés. Bizonyítható, hogy ha \(\displaystyle P\) az \(\displaystyle ABC\) szabályos háromszög bármely belső pontja, a \(\displaystyle PA, PB, PC\) szakaszokból akkor is szerkeszthető háromszög. Ekkor a feladatnak a háromszög egyik szögére vonatkozó állítása általános esetben már nem teljesül.

Statistics:

21 students sent a solution.
5 points:	Cynolter Dorottya, Deák Gergely, Fekete Patrik, Halász Henrik, Horváth Milán, Hosszu Noel, Keszthelyi Eszter, Kurucz Márton, Nagy Daniella, Pekk Márton, Sipeki Márton, Szabó Réka, Szabó Zóra, Szittyai Anna, Waldhauser Miklós, Werner Kinga.
3 points:	2 students.
1 point:	1 student.

Problems in Mathematics of KöMaL, April 2022