 |
A C. 1768. feladat (2023. május) |
C. 1768. Mutassuk meg, hogy a
$$\begin{align*} 8x^3+27y^3 & =-6\cdot5^3, \\ \frac{3}{x}+\frac{2}{y} & =\frac{xy}{5} \end{align*}$$egyenletrendszernek nincs megoldása, ha \(\displaystyle x\), \(\displaystyle y\) valós számok.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2023. június 12-én LEJÁRT.
1. megoldás. Tegyük fel a bizonyítandó állítás ellenkezőjét, eszerint vannak olyan \(\displaystyle x\), \(\displaystyle y\) valós számok, amelyek kielégítik az egyenletrendszer mindkét egyenletét.
Nyilvánvaló, hogy az \(\displaystyle x\), \(\displaystyle y\) számok egyike sem lehet 0. Az is könnyen látható, hogy ha van megoldás, akkor az \(\displaystyle x\), \(\displaystyle y\) valós számok csak ellenkező előjelűek lehetnek, mert ha mindkét szám pozitív, akkor az első egyenlet, ha pedig mindkettő negatív, akkor a második egyenlet nem teljesülhet.
Mivel \(\displaystyle 8x^3=(2x)^3\) és \(\displaystyle 27y^3=(3y)^3\), ezért az első egyenlet így is írható:
\(\displaystyle (2x)^3+(3y)^3=-6\cdot5^3,\)
ebből a \(\displaystyle a^3+b^3=(a+b)(a^2-ab+b^2)\) azonosság alapján az következik, hogy
| \(\displaystyle (1)\) | \(\displaystyle (2x+3y)(4x^2-6xy+9y^2)=-6\cdot5^3.\) |
A második egyenlet ekvivalens átalakításával \(\displaystyle 5(2x+3y)=(xy)^2\), innen pedig
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{2x+3y=\frac{(xy)^2}{5}}.\) |
A (2) összefüggésből láthatjuk, hogy \(\displaystyle 2x+3y\) pozitív szám, ezért, mivel (1) jobb oldala negatív, szükséges, hogy fennálljon
| \(\displaystyle (3)\) | \(\displaystyle 4x^2-6xy+9y^2<0.\) |
Osszuk el (3) mindkét oldalát a nyilván pozitív \(\displaystyle y^2\) kifejezéssel és legyen \(\displaystyle \displaystyle{\frac{x}{y}=z}\). Két nem nulla valós szám hányadosa is valós, tehát \(\displaystyle z\in R\), továbbá \(\displaystyle x\) és \(\displaystyle y\) ellenkező előjele miatt \(\displaystyle z<0\), így a (3)-ból kapott
| \(\displaystyle (4)\) | \(\displaystyle 4z^2-6z+9<0.\) |
egyenlőtlenség megoldásai, ha léteznek, akkor negatív valós számok.
A (4) egyenlőtlenség bal oldalán álló másodfokú kifejezés diszkriminánsa azonban \(\displaystyle D=-108\). Ezért az \(\displaystyle f(z)=4z^2-6z+9\) másodfokú függvény képe olyan felfelé nyíló parabola, amelynek nincs közös pontja a \(\displaystyle z\) tengellyel, ahogy az az alábbi ábrán látható.
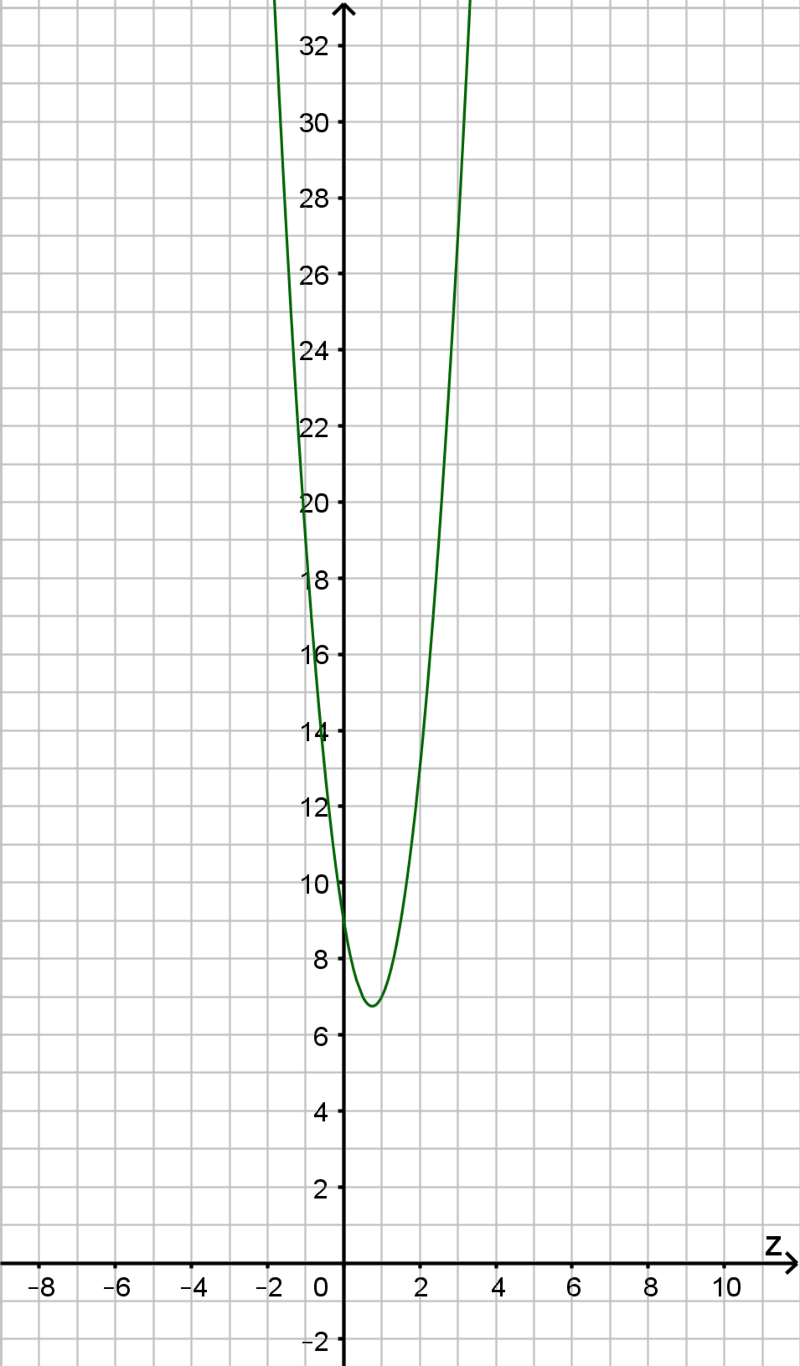
Ez pedig azt jelenti, hogy a (4) egyenlőtlenségnek nincs valós megoldása, de akkor a (3) egyenlőtlenségnek és az (1)-(2) egyenleteknek sincs valós megoldása. Feltevésünk tehát ellentmondásra vezetett, így az eredeti egyenletrendszernek valóban nincs megoldása, ha \(\displaystyle x\), \(\displaystyle y\) valós számok.
Megjegyzés. A (4) egyenlőtlenségben szereplő felfelé nyíló parabola csúcspontja a \(\displaystyle \displaystyle{C\Bigg(\frac{3}{4};\frac{27}{16}\Bigg)}\) pont.
2. megoldás. Kovács Béla (Szatmárnémeti) ötlete alapján
Tegyük fel, hogy az egyenletrendszernek van a valós számpárok halmazán megoldása.
A 2. egyenletből egyrészt látható, hogy az \(\displaystyle x\), \(\displaystyle y\) valós számok egyike sem lehet \(\displaystyle 0\), másrészt nem lehetséges, hogy \(\displaystyle x\) és \(\displaystyle y\) egyszerre negatívok, mert ebben az esetben az egyenlet két oldala ellenkező előjelű. Ebből az is következik, hogy vagy mindkét valós szám pozitív, és ezért \(\displaystyle xy>0\), vagy az egyik pozitív, a másik negatív, utóbbi esetben \(\displaystyle xy<0\).
Felhasználjuk az 1. megoldás (1) és (2) összefüggését, amely szerint
\(\displaystyle \displaystyle{(2x+3y)(4x^2-6xy+9y^2)=-6\cdot5^3; \qquad 2x+3y=\frac{(xy)^2}{5}}.\)
Megmutatjuk, hogy ez a két egyenlet egyszerre nem teljesülhet.
A második egyenlet szerint \(\displaystyle 2x+3y>0\), így, mivel az első egyenlet jobb oldala negatív, ezért a \(\displaystyle 4x^2-6xy+9y^2\) kifejezésnek negatívnak kell lennie.
Ugyanakkor, a fentiek szerint, ha \(\displaystyle x>0\) és \(\displaystyle y>0\), akkor \(\displaystyle xy>0\), és ezért a \(\displaystyle 4x^2-6xy+9y^2=(2x-3y)^2+6xy\) egyenlőség miatt \(\displaystyle 4x^2-6xy+9y^2>0\).
Ha pedig \(\displaystyle x\) és \(\displaystyle y\) ellenkező előjelűek, akkor \(\displaystyle xy<0\), tehát a \(\displaystyle 4x^2-6xy+9y^2\) kifejezés minden tényezője pozitív, vagyis ismét teljesül, hogy \(\displaystyle 4x^2-6xy+9y^2>0\).
Ellentmondásra jutottunk, ezért az egyenletnek a valós számpárok halmazán valóban nincs megoldása.
Megjegyzés. Könnyen belátható, hogy ha az első egyenlet jobb oldalán bármilyen negatív valós szám áll, akkor a második egyenlet változatlanul hagyása mellett az egyenletrendszernek nincs megoldása.
Statisztika:
79 dolgozat érkezett. 5 pontot kapott: Aaishipragya Kahaly, Baksa Anna, Baran Júlia, Bettesch Emma Léda, Blaskovics Ádám, Braun Zsófia, Ehrlich Máté, Fiser 234 Boldizsár, Holczer Kenéz, Iván Máté Domonkos, Kerekes András, Keszthelyi Eszter, Kiss Máté, Klement Tamás, Kószó Ferenc, Ligeti Ábel, Mészáros Anna Veronika, Monoczki Máté, Németh Hanna Júlia , Papp Zsófia, Raffay Gergely, Seprődi Barnabás Bendegúz, Simon Bálint, Sipeki Márton, Somogyi Dóra, Sütő Áron, Szabó Donát, Szegedi Ágoston, Teveli Jakab, Tomesz László Gergő, Tömböly 299 Áron, Török Eszter Júlia, Ujpál Bálint, Végh Lilian, Volford Barnabás, Waldhauser Miklós, Wodala Gréta Klára. 4 pontot kapott: 21 versenyző. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 5 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2023. májusi matematika feladatai

