 |
A C. 1792. feladat (2023. december) |
C. 1792. Az \(\displaystyle ABC\) háromszög \(\displaystyle AB\) és \(\displaystyle AC\) oldalának felezőpontja \(\displaystyle F\), illetve \(\displaystyle E\). Legyen \(\displaystyle P\) és \(\displaystyle Q\) a háromszög síkjának tetszőleges két pontja. A \(\displaystyle P\) pontnak az \(\displaystyle E\)-re, a \(\displaystyle Q\) pontnak az \(\displaystyle F\)-re vonatkozó tükörképe legyen \(\displaystyle P'\), illetve \(\displaystyle Q'\). A \(\displaystyle PB\) szakasz felezőpontja \(\displaystyle M\), a \(\displaystyle QC\) szakasz felezőpontja \(\displaystyle N\). Bizonyítsuk be, hogy \(\displaystyle MN\parallel P'Q'\) és \(\displaystyle P'Q'=2MN\).
Javasolta: Van Khea (Kambodzsa)
(5 pont)
A beküldési határidő 2024. január 10-én LEJÁRT.
Megoldás. Helyezzük az \(\displaystyle ABC\) háromszöget a derékszögű koordináta-rendszerbe és legyenek az \(\displaystyle A,B,C\) pontok koordinátái
\(\displaystyle A(a_1, a_2);\qquad B(b_1,b_2); \qquad C(c_1,c_2),\)
ezzel az \(\displaystyle E\) és \(\displaystyle F\) pontok koordinátáira
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{E\Big(\frac{a_1+c_1}{2}, \frac{a_2+c_2}{2}\Big);\qquad F\Big(\frac{a_1+b_1}{2}, \frac{a_2+b_2}{2}\Big)}.\) |
Tekintsük a következő ábrát.
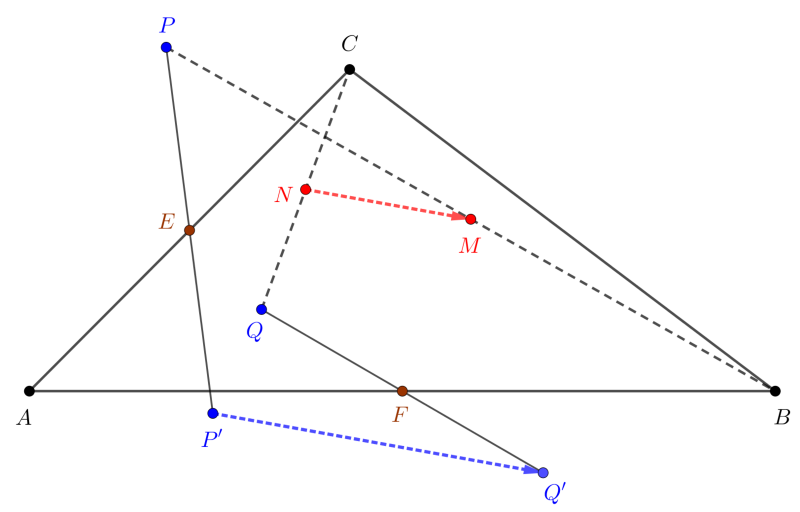
Ha a \(\displaystyle P\) és \(\displaystyle Q\) pontok koordinátái \(\displaystyle P(p_1,p_2)\) illetve \(\displaystyle Q(q_1,q_2)\), akkor, mivel a \(\displaystyle PP'\) és \(\displaystyle AC\) szakaszok közös felezőpontja \(\displaystyle E\), ezért (1) alapján \(\displaystyle \displaystyle{\frac{p_1+p'_1}{2}=\frac{a_1+c_1}{2}}\), illetve \(\displaystyle \displaystyle{\frac{p_2+p'_2}{2}=\frac{a_2+c_2}{2}}\).
Hasonlóképpen a \(\displaystyle QQ'\) és \(\displaystyle AB\) szakaszok közös felezőpontja \(\displaystyle F\), így \(\displaystyle \displaystyle{\frac{q_1+q'_1}{2}=\frac{a_1+b_1}{2}}\), illetve \(\displaystyle \displaystyle{\frac{q_2+q'_2}{2}=\frac{a_2+b_2}{2}}\).
Ebből egyszerű számolással adódik a \(\displaystyle P'\) és \(\displaystyle Q'\) pontok koordinátáira, hogy
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{P'\big(a_1+c_1-p_1; a_2+c_2-p_2\big),\qquad Q'\big(a_1+b_1-q_1; a_2+b_2-q_2\big)}.\) |
A \(\displaystyle PB\), illetve \(\displaystyle QC\) szakaszok felezőpontja \(\displaystyle M\), illetve \(\displaystyle N\), ezért
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{M\Big(\frac{p_1+b_1}{2}; \frac{p_2+b_2}{2}\Big),\qquad N\Big(\frac{q_1+c_1}{2}; \frac{q_2+c_2}{2}\Big)}.\) |
A kezdő-és végpontok koordinátái és a (2), illetve (3) összefüggések segítségével felírjuk a \(\displaystyle \overrightarrow{P'Q'}\) és \(\displaystyle \overrightarrow{NM}\) vektorok koordinátáit:
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{\overrightarrow{P'Q'}\big(b_1-c_1+p_1-q_1; b_2-c_2+p_2-q_2\big),\qquad \overrightarrow{NM}\Big(\frac{b_1-c_1+p_1-q_1}{2}; \frac{b_2-c_2+p_2-q_2}{2}\Big)}.\) |
A (4) összefüggés azt mutatja, hogy a \(\displaystyle \overrightarrow{P'Q'}\) vektor koordinátáit az \(\displaystyle \overrightarrow{NM}\) vektor megfelelő koordinátáinak kettővel való szorzása révén kapjuk. Ez egyrészt azt jelenti, hogy a \(\displaystyle \overrightarrow{P'Q'}\) vektor egyirányú az \(\displaystyle \overrightarrow{NM}\) vektorral, vagyis valóban teljesül, hogy a \(\displaystyle P'Q'\) egyenes párhuzamos az \(\displaystyle MN\) egyenessel.
Másrészt a vektorok hosszára vonatkozó ismeretek alapján (4)-ből az is adódik, hogy \(\displaystyle \Big|\overrightarrow{P'Q'}\Big|=2\cdot \Big|\overrightarrow{NM}\Big|\), azaz a \(\displaystyle P'Q'=2MN\) is fennáll. Ezzel a feladat mindkét állítását igazoltuk.
Megjegyzés. Könnyen igazolható, hogy a feladat állítása akkor is igaz, ha \(\displaystyle A,B,C\) és \(\displaystyle P,Q\) tetszőleges térbeli pontok.
Statisztika:
42 dolgozat érkezett. 5 pontot kapott: Baksa Anna, Balogh Péter, Barna Márton, Braun Zsófia, Csiszár András, Göőz Lilla, Gyuricsek Ákos, Inokai Ádám, Iván Máté Domonkos, Márfai Dóra, Masa Barnabás, Mayer Péter, Medgyesi Júlia, Nagy 292 Korina, Németh Hanna Júlia , Simon Bálint, Szabó Donát, Tóth-Falusi Mihály, Török Eszter Júlia, Ujpál Bálint, Wodala Gréta Klára. 4 pontot kapott: Harmincz Sára, Pánovics Máté, Veres Zsombor Gábor, Volford Barnabás. 3 pontot kapott: 4 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2023. decemberi matematika feladatai

