 Problem C. 1822. (September 2024)
Problem C. 1822. (September 2024)
C. 1822. The diagonals \(\displaystyle AC\) and \(\displaystyle BD\) of convex quadrilateral \(\displaystyle ABCD\) intersect each other at point \(\displaystyle M\). Let positive integers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) and \(\displaystyle d\) be the areas of the resulting triangles \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\) and \(\displaystyle DAM\), respectively.
\(\displaystyle a)\) Prove that the product \(\displaystyle a\cdot b\cdot c\cdot d\) is a perfect square.
\(\displaystyle b)\) Suppose that there are exactly two distinct odd primes among \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) and \(\displaystyle d\). Find the values of \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) and \(\displaystyle d\) such that the area of the quadrilateral \(\displaystyle ABCD\) is the smallest possible perfect square.
Proposed by Bíró Bálint, Eger
(5 pont)
Deadline expired on October 10, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) Tekintsük az alábbi ábrát.
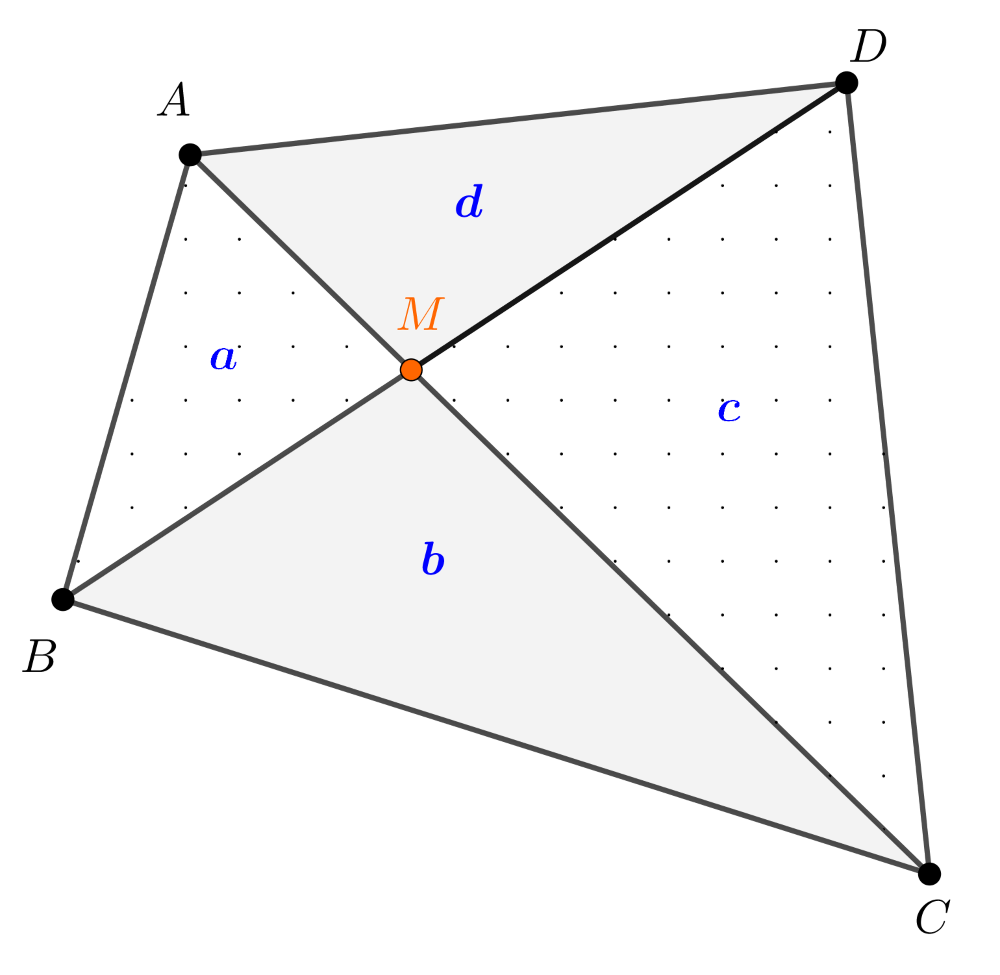
Az \(\displaystyle ABM\) és \(\displaystyle BCM\) háromszögeknek a \(\displaystyle B\) csúcshoz tartozó magassága közös, ezért területeik aránya az \(\displaystyle AM\) és \(\displaystyle BM\) alapok hosszának arányával egyezik meg, azaz
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{\frac{a}{b}=\frac{AM}{MC}}.\) |
Hasonlóképpen a \(\displaystyle DAM\) és \(\displaystyle CDM\) háromszögeknek a \(\displaystyle D\) csúcshoz tartozó magassága közös, tehát területeik aránya a megfelelő alapok hosszának arányával egyenlő, vagyis
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{\frac{d}{c}=\frac{AM}{MC}}.\) |
Az (1) és (2) eredmények szerint
\(\displaystyle \displaystyle{\frac{a}{b}=\frac{d}{c}},\)
ezért
| \(\displaystyle (3)\) | \(\displaystyle a\cdot c=b\cdot d. \) |
(3) viszont azt jelenti, hogy \(\displaystyle a\cdot{c}\cdot{b}\cdot{d}=(a\cdot{c})^2=(b\cdot{d})^2\), és mivel \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) pozitív egészek, ezért \(\displaystyle a\cdot c\cdot b\cdot d\) valóban négyzetszám.
\(\displaystyle b)\) Nem sérti az általánosságot, ha feltesszük, hogy az \(\displaystyle a\) prímszám. Ekkor két lehetséges eset van:
1) \(\displaystyle b\) és \(\displaystyle d\) közül pontosan az egyik prím,
vagy
2) \(\displaystyle c\) prímszám.
Tekintsük először az 1) esetet.
Feltehetjük, hogy \(\displaystyle d\) prímszám, ekkor a feltételnek megfelelően \(\displaystyle b\) és \(\displaystyle c\) nem prímek. Az \(\displaystyle a)\) feladatrészben igazoltuk, hogy
\(\displaystyle a\cdot c=b\cdot d,\)
ebből az következik, hogy a \(\displaystyle d\) prím osztója a \(\displaystyle c\) számnak, hiszen \(\displaystyle a\)-nak nem lehet osztója, mivel \(\displaystyle a\) és \(\displaystyle d\) különböző prímek.
Ezért
\(\displaystyle c=k\cdot d, \)
ahol \(\displaystyle k\neq{1}\), hiszen \(\displaystyle c\) nem prím.
Ekkor azonban az \(\displaystyle a\cdot c=b\cdot d\) összefüggésből azt kapjuk, hogy
\(\displaystyle b=k\cdot a.\)
Az \(\displaystyle ABCD\) négyszög \(\displaystyle T\) területére teljesül, hogy
\(\displaystyle T=a+b+c+d,\)
ebből előző eredményeink alapján \(\displaystyle T=a+k\cdot a+k\cdot d+d\) adódik, amelyből szorzattá alakítás után következik, hogy
| \(\displaystyle (4)\) | \(\displaystyle T=(a+d)\cdot(k+1).\) |
A \(\displaystyle T\) szám négyzetszám kell legyen, mégpedig a feltételek és annak figyelembe vételével, hogy \(\displaystyle a+d\) páros, a lehető legkisebb páros négyzetszám.
Kézenfekvő tehát, hogy kis értékű páratlan \(\displaystyle a\), \(\displaystyle d\) prímeket keressünk.
Az általánosság megsértése nélkül feltehető, hogy \(\displaystyle a<d\), ezért ha például \(\displaystyle a=3\) és \(\displaystyle d=5\), akkor \(\displaystyle a+d=8\), így \(\displaystyle k+1=2\) esetén azt kapjuk, hogy \(\displaystyle T=16\), amely négyzetszám ugyan, de ez mégsem felel meg a feltételeknek, hiszen ekkor \(\displaystyle k=1\) lenne. Így \(\displaystyle a=3\) és \(\displaystyle d=5\) mellett \(\displaystyle k+1\) értéke legalább \(\displaystyle 8\), azaz \(\displaystyle T\) legalább \(\displaystyle 64\).
Egyszerű számolással beláthatjuk, hogy ennél kisebb \(\displaystyle T\) négyzetszámot csak akkor kaphatunk, ha
\(\displaystyle a=5, \quad d=7,\)
ekkor \(\displaystyle k+1=3\), vagyis \(\displaystyle k=2\) mellett
| \(\displaystyle (5)\) | \(\displaystyle T=36.\) |
Tekintsük most a 2) lehetőséget, vagyis azt, amikor \(\displaystyle a\) mellett \(\displaystyle c\) a másik prímszám, itt is feltehetjük, hogy \(\displaystyle a<c\).
Ebből egyrészt az következik, hogy \(\displaystyle b\) és \(\displaystyle d\) egyike sem prím, másrészt \(\displaystyle a\cdot c=b\cdot d\) alapján \(\displaystyle b\cdot d\) két prím szorzata, amely csak úgy állhat fenn, ha a \(\displaystyle b\) és \(\displaystyle d\) közül valamelyik szám értéke \(\displaystyle 1\).
Legyen például \(\displaystyle b=1\), ekkor nyilvánvaló, hogy
| \(\displaystyle (6)\) | \(\displaystyle d=a\cdot c.\) |
Mivel \(\displaystyle T\) értékére ismét a lehető legkisebb négyzetszámot keressük, ezért \(\displaystyle a=3, c=5\) és \(\displaystyle b=1\) mellett (6) szerint \(\displaystyle d=15\), ekkor azonban
\(\displaystyle T=3+1+5+15=24,\)
ez viszont nem négyzetszám. Ha pedig \(\displaystyle a=3, c=7\) és \(\displaystyle b=1\) mellett \(\displaystyle d=21\), akkor
\(\displaystyle T=3+1+7+21=32,\)
de ez sem négyzetszám.
Könnyen belátható, hogy bármely más \(\displaystyle a\), \(\displaystyle c\) prímek és \(\displaystyle b=1\) esetén a \(\displaystyle T\) számra \(\displaystyle 36\)-nál nagyobb értéket kapunk.
Minden esetet megvizsgáltunk, és azt kaptuk, hogy a feladat feltételeinek az
\(\displaystyle a=5, \,d=7,\)
illetve \(\displaystyle k=2\) miatt
\(\displaystyle b=10,\, c=14\)
számok felelnek meg, így
\(\displaystyle T=36.\)
Megjegyzések. 1) Az (5) eredmény \(\displaystyle a=5, d=13\) illetve \(\displaystyle a=7, d=11\) esetén is elérhető, de mindkét esetben \(\displaystyle k=1\), ezért ezekből nem kapunk megoldást.
2) A feltételeknek megfelelő \(\displaystyle ABCD\) négyszög valóban létezik. Ha például \(\displaystyle AC\) merőleges \(\displaystyle BD\)-re és \(\displaystyle AM=5\), \(\displaystyle CM=10\), illetve \(\displaystyle BM=2\), valamint \(\displaystyle \displaystyle{DM=\frac{14}{5}}\), akkor az \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\), \(\displaystyle DAM\) háromszögek területe rendre \(\displaystyle 5\), \(\displaystyle 10\), \(\displaystyle 14\), \(\displaystyle 7\).
Statistics:
55 students sent a solution. 5 points: Balog 888 Emese, Balogh Péter, Barna Márton, Budai Máté, Iván Máté Domonkos, Kókai Ákos, Masa Barnabás, Monoczki Máté, Pink István, Wodala Gréta Klára. 4 points: Bencze Mátyás, Márfai Dóra. 3 points: 15 students. 2 points: 15 students. 1 point: 4 students. 0 point: 2 students. Not shown because of missing birth date or parental permission: 2 solutions.
Problems in Mathematics of KöMaL, September 2024
