 |
A C. 1841. feladat (2025. január) |
C. 1841. A \(\displaystyle PQRS\) konvex négyszögben \(\displaystyle QR=4\), \(\displaystyle RS=6\), \(\displaystyle SP=5\), és a \(\displaystyle P\), illetve \(\displaystyle Q\) csúcsoknál levő belső szögek \(\displaystyle 60^{\circ}\)-osak. Ha tudjuk, hogy \(\displaystyle 2PQ=a+\sqrt{b}\), ahol \(\displaystyle a\) és \(\displaystyle b\) pozitív egészek, akkor határozzuk meg az \(\displaystyle a+b\) összeg értékét.
(ausztrál versenyfeladat)
(5 pont)
A beküldési határidő 2025. február 10-én LEJÁRT.
Megoldás. A feltételek miatt \(\displaystyle SPQ\sphericalangle=PQR\sphericalangle=60^{\circ}\), ezért a \(\displaystyle PS\) és \(\displaystyle QR\) félegyenesek a \(\displaystyle PQ\) egyenes ugyanazon oldalán vannak és metszik egymást egy pontban, legyen ez a pont \(\displaystyle T\). Tekintsük az alábbi ábrát, amelyen az \(\displaystyle RT=x\) és \(\displaystyle ST=y\) további jelöléseket alkalmaztuk.
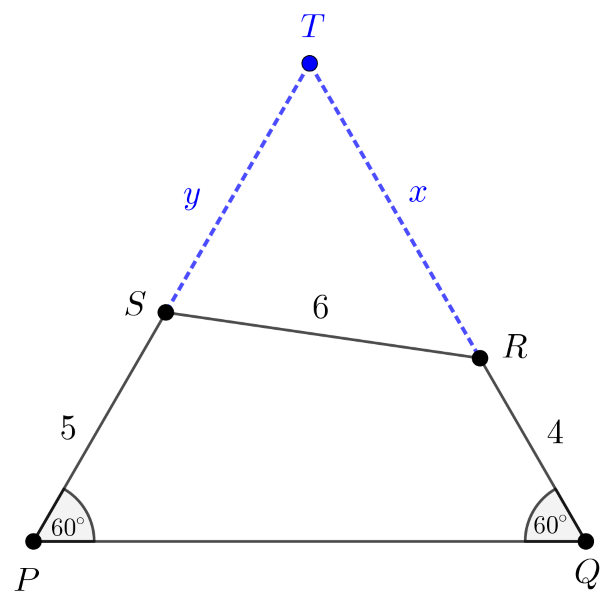
Nyilvánvaló, hogy \(\displaystyle QTP\sphericalangle=60^{\circ}\), vagyis a \(\displaystyle PQT\) háromszög szabályos, amelynek \(\displaystyle PQ\) oldalára a feltétel szerint \(\displaystyle \displaystyle{PQ=\frac{a+\sqrt{b}}{2}}\) teljesül. A szabályos háromszög oldalhosszai egyenlők, ezért
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{x+4=y+5=\frac{a+\sqrt{b}}{2}}.\) |
Felírjuk a koszinusztételt a \(\displaystyle TSR\) háromszögre, eszerint: \(\displaystyle x^2+y^2-2xy\cdot \cos 60^{\circ}=36\), amiből \(\displaystyle \displaystyle{\cos60^{\circ}=\frac{1}{2}}\) miatt
| \(\displaystyle (2)\) | \(\displaystyle x^2+y^2-xy=36\) |
következik.
Az (1) egyenlet miatt \(\displaystyle y=x-1\), így ezt (2)-be írva, a műveletek elvégzése és rendezés után az
\(\displaystyle x^2-x-35=0\)
másodfokú egyenletet kapjuk, amelynek gyökei
\(\displaystyle \displaystyle{x_1=\frac{1+\sqrt{141}}{2};\quad x_2=\frac{1-\sqrt{141}}{2}}.\)
Mivel \(\displaystyle x>0\), ezért \(\displaystyle x_2\) nyilván nem megoldás.
Az \(\displaystyle x_1\) értékét az (1) egyenletbe írva \(\displaystyle \displaystyle{\frac{1+\sqrt{141}}{2}+4=\frac{a+\sqrt{b}}{2}}\), ahonnan átrendezés után azt kapjuk, hogy
| \(\displaystyle (3)\) | \(\displaystyle 9+\sqrt{141}=a+\sqrt{b}.\) |
A \(\displaystyle 9+\sqrt{141}\) szám egyértelműen írható fel \(\displaystyle a\) és \(\displaystyle b\) pozitív egészekkel \(\displaystyle a+\sqrt{b}\) alakban, ezért a (3) egyenletből \(\displaystyle a+b=9+141=150\).
Ezzel a feladatot megoldottuk.
Statisztika:
33 dolgozat érkezett. 5 pontot kapott: Albert Luca Liliána, Balogh Péter, Bán Kincső Panni, Barna 201 Krisztina, Bencze Mátyás, Budai Máté, Hetyei Dániel, Hodossy-Takács Ráhel, Iván Máté Domonkos, Kókai Ákos, Masa Barnabás, Medgyesi Júlia, Molnár Lili, Móricz Zsombor, Pánovics Máté, Pink István, Rózsa Zsombor, Sebők Violetta Írisz, Száva András. 4 pontot kapott: Bernáth Csenge, Farkas Máté, Kulcsár Anna Zita, Mágori Zsanett. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2025. januári matematika feladatai
