 |
A C. 1864. feladat (2025. szeptember) |
C. 1864. Egy hatszög szögei egyenlők, négy egymást követő oldalának hossza \(\displaystyle 5\), \(\displaystyle 3\), \(\displaystyle 6\) és \(\displaystyle 7\) (ebben a sorrendben). Számítsuk ki a következő két oldal hosszát.
indiai versenyfeladat
(5 pont)
A beküldési határidő 2025. október 10-én LEJÁRT.
Megoldás. Legyen az \(\displaystyle ABCDEF\) hatszögben \(\displaystyle AB=5\), \(\displaystyle BC=3\), \(\displaystyle CD=6\), \(\displaystyle DE=7\) és \(\displaystyle EF=x\), \(\displaystyle FA=y\). A hatszög pontosan négy háromszögre bontható, így belső szögeinek összege \(\displaystyle 4\cdot 180^{\circ}=720^{\circ}\).
Mivel a feltétel szerint a belső szögek egyenlők, ezért például az \(\displaystyle A\) csúcsnál levő belső szöget \(\displaystyle \alpha\)-val jelölve \(\displaystyle 6\cdot \alpha=720^{\circ}\), azaz a belső szögek mindegyike \(\displaystyle \alpha=120^{\circ}\). Ez egyúttal azt is jelenti, hogy \(\displaystyle ABCDEF\) konvex hatszög.
Mivel \(\displaystyle ABC\sphericalangle=BCD\sphericalangle=120^{\circ}\), ezért a hatszög \(\displaystyle B\), illetve \(\displaystyle C\) csúcsánál levő külső szögek egyaránt \(\displaystyle 60^{\circ}\)-osak, így az \(\displaystyle AB\) és \(\displaystyle CD\) egyenesek a \(\displaystyle 3\) egység oldalú \(\displaystyle BGC\) szabályos háromszöget zárják közre.
Hasonlóan látható be, hogy a \(\displaystyle CD\) és \(\displaystyle EF\) a \(\displaystyle 7\) egység oldalú \(\displaystyle DHE\), az \(\displaystyle EF\) és \(\displaystyle AB\) egyenesek pedig az \(\displaystyle y\) egység oldalú \(\displaystyle FKA\) szabályos háromszöget zárják közre. Tekintsük az alábbi ábrát.
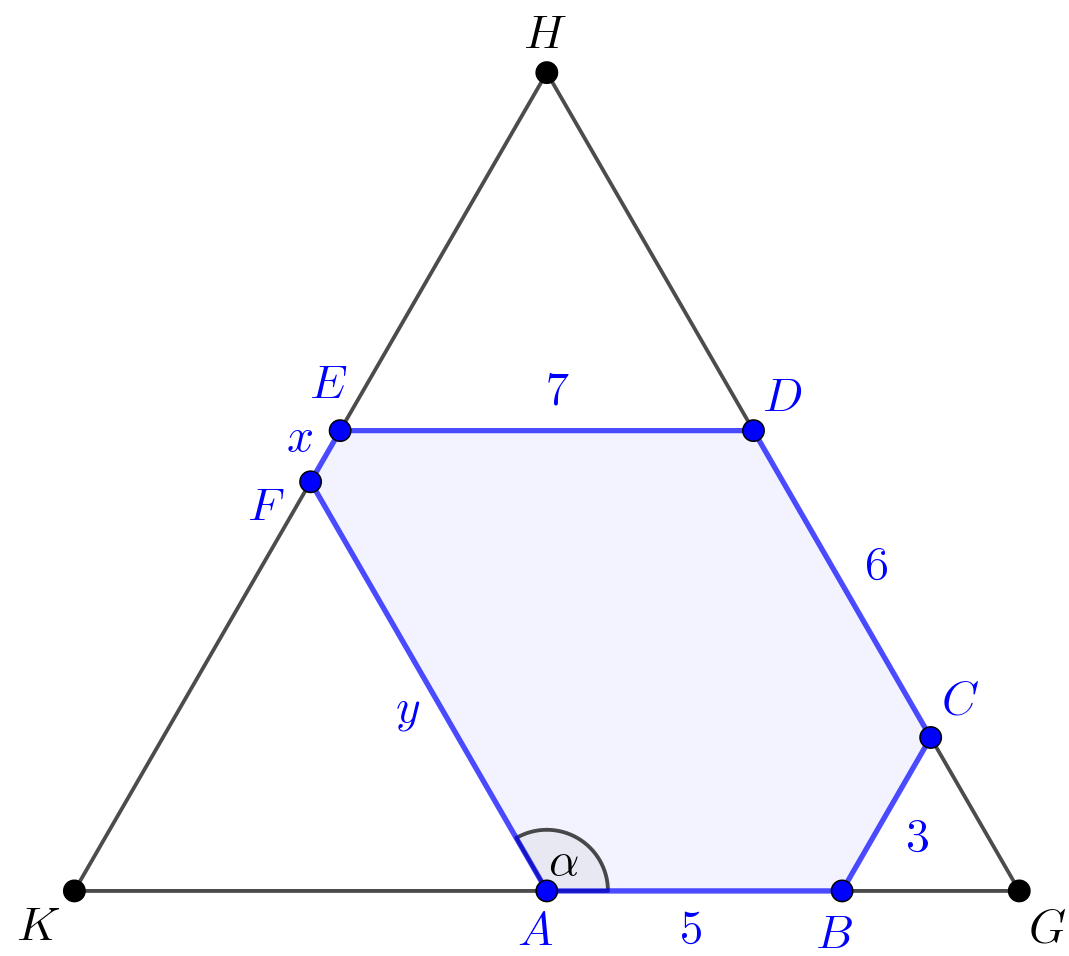
A fentiekből az is következik, hogy \(\displaystyle GHK\) is szabályos háromszög, ezért oldalai egyenlő hosszúak, eszerint
\(\displaystyle y+5+3=3+6+7,\)
illetve
\(\displaystyle 7+x+y=3+6+7.\)
Az első egyenletből \(\displaystyle y=8\), ennek alapján a második egyenletből \(\displaystyle x=1\) adódik.
Az \(\displaystyle ABCDEF\) hatszög két oldalának hossza tehát \(\displaystyle x=1, y=8\). Ezzel a megoldást befejeztük.
Megjegyzések. 1) Könnyen belátható, hogy az \(\displaystyle ABCDEF\) hatszögben \(\displaystyle AB\parallel {DE}; BC\parallel {EF}; CD\parallel {FA}\) és emiatt a hatszög paralelogrammává is kiegészíthető. Ezzel az eljárással is az \(\displaystyle x=1, y=8\) eredményhez jutunk.
2) A szemben levő oldalak párhuzamosságának következményeként bizonyítható például az is, hogy a \(\displaystyle ACE\) és \(\displaystyle BDF\) háromszögek területe egyenlő.
Statisztika:
230 dolgozat érkezett. 5 pontot kapott: 56 versenyző. 4 pontot kapott: 75 versenyző. 3 pontot kapott: 27 versenyző. 2 pontot kapott: 19 versenyző. 1 pontot kapott: 22 versenyző. 0 pontot kapott: 29 versenyző.
A KöMaL 2025. szeptemberi matematika feladatai

