A C. 1866. feladat (2025. szeptember)

C. 1866. Adott egy egységnyi hosszúságú, illetve egy \(\displaystyle a\) és egy \(\displaystyle b\) hosszúságú (\(\displaystyle a\neq 1\) és \(\displaystyle b\neq 1\)) szakasz. Adjunk szerkesztési eljárást az \(\displaystyle \dfrac{1}{a}\), az \(\displaystyle a\cdot b\) és az \(\displaystyle a^2\cdot b^3\) hosszúságú szakaszok szerkesztésére. (Az elemi szerkesztési lépéseket, mint például szög felezése, tengelyes tükrözés, nem kell részletezni.)

Javasolta: Bíró Bálint (Eger)

(5 pont)

A beküldési határidő 2025. október 10-én LEJÁRT.

Megoldás. Az alábbi euklideszi szerkesztési lépések során mindvégig feltételezzük, hogy olyan vonalzónk van, amellyel tetszőleges hosszúságú egyenes szakaszt rajzolhatunk és olyan körzővel rendelkezünk, amellyel tetszőleges sugarú kört szerkeszthetünk.

A szerkesztési feladatokat a párhuzamos szelők tételének alkalmazásával oldjuk meg. Az \(\displaystyle \displaystyle{\frac{1}{a}}\) hosszúságú szakasz megszerkesztéséhez egy \(\displaystyle O\) csúcsú \(\displaystyle \varphi\) szög egyik szárára felmérjük az \(\displaystyle a\) hosszúságú \(\displaystyle OA\) szakaszt, majd az \(\displaystyle OA\) félegyenesre az \(\displaystyle A\) ponton túl az egységnyi hosszú \(\displaystyle AB\) szakaszt, végül a szög másik szárára felmérjük egységnyi hosszú \(\displaystyle OA'\) szakaszt.

Ezután a \(\displaystyle B\) ponton keresztül párhuzamost szerkesztünk az \(\displaystyle AA'\) egyenessel, amely az \(\displaystyle OA'\) egyenest a \(\displaystyle B'\) pontban metszi (1. ábra).

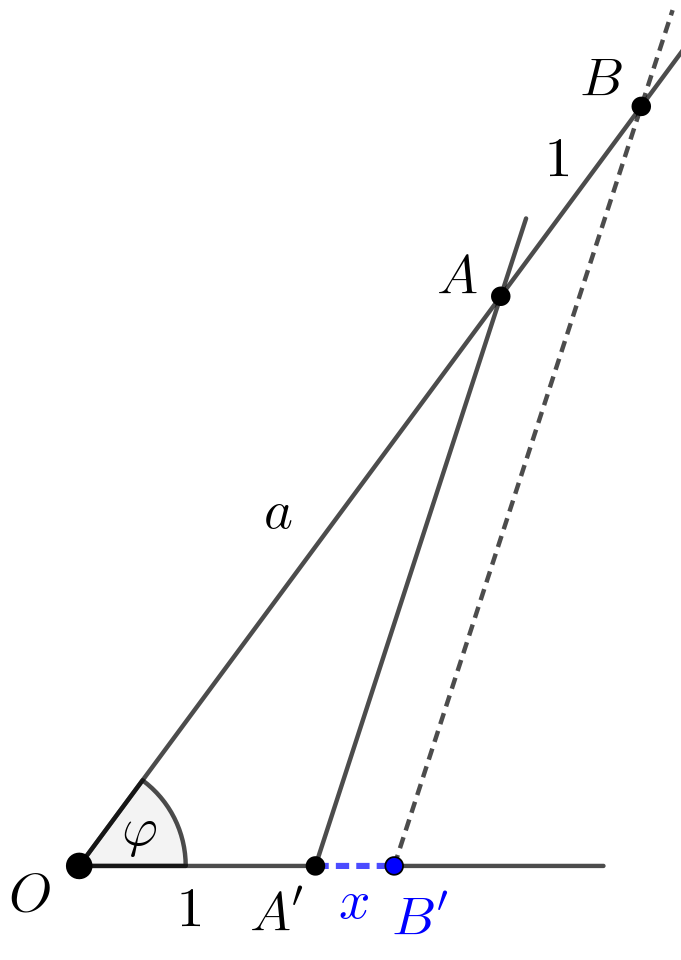
1. ábra

A szög szárain keletkezett szakaszok hosszára felírhatjuk a párhuzamos szelők tételét: \(\displaystyle \displaystyle{\frac{OA}{AB}=\frac{OA'}{A'B'}}\), azaz \(\displaystyle \displaystyle{\frac{a}{1}=\frac{1}{x}}\), ahonnan \(\displaystyle \displaystyle{x=\frac{1}{a}}\), ezzel megszerkesztettük az \(\displaystyle \displaystyle{\frac{1}{a}}\) hosszúságú \(\displaystyle A'B'\) szakaszt.

Az \(\displaystyle a\cdot b\) hosszúságú szakasz megszerkesztéséhez egy \(\displaystyle O\) csúcsú, az előző szöggel nem feltétlenül azonos szög egyik szárára felmérjük az \(\displaystyle OC=1\), ezután a \(\displaystyle CD=b\), a másik szárára pedig az \(\displaystyle OC'=a\) szakaszt, majd a \(\displaystyle D\) ponton keresztül párhuzamost szerkesztünk a \(\displaystyle CC'\) egyenessel, amely az \(\displaystyle OC'\) egyenest a \(\displaystyle D'\) pontban metszi (2. ábra).

2. ábra

A párhuzamos szelők tétele szerint \(\displaystyle \displaystyle{\frac{OC}{CD}=\frac{OC'}{C'D'}}\), vagyis \(\displaystyle \displaystyle{\frac{1}{b}=\frac{a}{y}}\), ahonnan \(\displaystyle \displaystyle{y=a\cdot b}\), így tehát megszerkesztettük az \(\displaystyle \displaystyle{a\cdot b}\) hosszúságú \(\displaystyle C'D'\) szakaszt is.

Az \(\displaystyle a^2\cdot b^3\) hosszúságú szakasz megszerkesztéséhez először megszerkesztjük az \(\displaystyle a^2\) hosszúságú szakaszt. Ehhez a 2. ábra szerinti lépéseket használjuk azzal a különbséggel, hogy a \(\displaystyle CD=b\) helyett a \(\displaystyle CE=a\) szakaszt mérjük fel a szög szárára.
A \(\displaystyle CC'\)-vel az \(\displaystyle E\) ponton át húzott párhuzamos az \(\displaystyle OC'\) egyenest olyan \(\displaystyle E'\) pontban fogja metszeni, amelyre \(\displaystyle C'E'=a^2\).
Ugyanezzel a módszerrel szerkeszthetjük meg előbb a \(\displaystyle b^2\), majd a \(\displaystyle b\cdot b^2=b^3\) hosszúságú szakaszokat.
Végül pedig a már megszerkesztett \(\displaystyle a^2\) és \(\displaystyle b^3\) hosszúságú szakaszokra alkalmazzuk a 2. ábrának megfelelő szerkesztési eljárást, vagyis \(\displaystyle CD=b\) helyett a \(\displaystyle CF=b^3\) szakaszt, a másik szögszárra pedig \(\displaystyle OC'=a\) helyett az \(\displaystyle OG'=a^2\) szakaszt mérjük fel. A \(\displaystyle CG'\)-vel az \(\displaystyle F\) ponton keresztül rajzolt párhuzamos olyan \(\displaystyle F'\) pontban metszi az \(\displaystyle OC'\) egyenesét, amelyre \(\displaystyle G'F'=a^2\cdot b^3\).

Ezzel a megoldást befejeztük.

Statisztika:

51 dolgozat érkezett.
5 pontot kapott:	Budai Máté, Farkas Noémi , Fülöp Magdaléna, Guirguis Mariam Mourad Fawzy Youssef, Halmosi Dávid, Hetyei Dániel, Ivák László, Jureczky Ákos, Király Zsuzsanna , Kókai Ákos, Kun Petra, Lupkovics Lázár, Márfai Lili, Masa Izabella, Mateas Isabelle, Nelissen Sámuel Zalán, Poczai Dorottya, Schneider Péter, Szabó Máté, Válek Péter, Varga 137 Levente, Viczián Adél.
4 pontot kapott:	Aaishipragya Kahaly, Albert Luca Liliána, Berei Gergő, Hirmann Dorottya, Kámán-Gausz Péter, Móricz Zsombor, Németh Ábel, Ördög Dominik, Papp Emese Petra, Pivárcsik Márk, Serfőző Dávid, Sipos Dániel Sándor, Szabó Medárd.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	6 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2025. szeptemberi matematika feladatai