 |
A C. 1874. feladat (2025. november) |
C. 1874. Adott két pont a síkon, \(\displaystyle G\) és \(\displaystyle H\). Szerkesszünk olyan hegyesszögű, egyenlő szárú háromszöget, amelynek magasságpontja \(\displaystyle H\), súlypontja \(\displaystyle G\). (Az elemi szerkesztési lépéseket, mint pl. szög felezése, tengelyes tükrözés, nem kell részletezni.)
Javasolta: Barta-Zágoni Csongor (Marosvásárhely)
(5 pont)
A beküldési határidő 2025. december 10-én LEJÁRT.
Nyilvánvaló, hogy mivel a feladatban két adott pontról van szó, ezért a \(\displaystyle H\) és \(\displaystyle G\) pontok nem lehetnek azonosak, tehát a szerkesztendő háromszög nem lehet egyenlő oldalú. Legyenek a szerkesztendő egyenlő szárú háromszög csúcsai \(\displaystyle A, B, C\), a háromszög szárai pedig \(\displaystyle AB=AC\). Az \(\displaystyle ABC\) háromszög pontosan akkor hegyesszögű, ha a megadott \(\displaystyle H\) magasság-és \(\displaystyle G\) súlyponton kívül a háromszög körülírt körének \(\displaystyle O\) középpontja is a háromszög belső pontja.
Az \(\displaystyle AB=AC\) egyenlőség miatt a \(\displaystyle H\), \(\displaystyle G\), \(\displaystyle O\) pontok mindegyike rajta van a \(\displaystyle BC\) szakasz felezőmerőlegesén. Jelöljük a \(\displaystyle H\) és \(\displaystyle G\) pontok távolságát \(\displaystyle 2d\)-vel. Ismert, hogy a \(\displaystyle G\) súlypont a \(\displaystyle HO\) szakasznak az \(\displaystyle O\)-hoz közelebb eső harmadolópontja, azaz
\(\displaystyle \displaystyle{\frac{OG}{GH}=\frac{1}{2}},\)
ezért
| \(\displaystyle (1)\) | \(\displaystyle OG=d.\) |
Legyen a \(\displaystyle HG\) egyenes és \(\displaystyle BC\) közös pontja \(\displaystyle D\) és \(\displaystyle OD=x\).
A \(\displaystyle D\) pontot fogjuk megszerkeszteni, amelyhez felvesszük a körülírt kör \(\displaystyle OA=R\) sugarát. Tekintsük a következő ábrát:
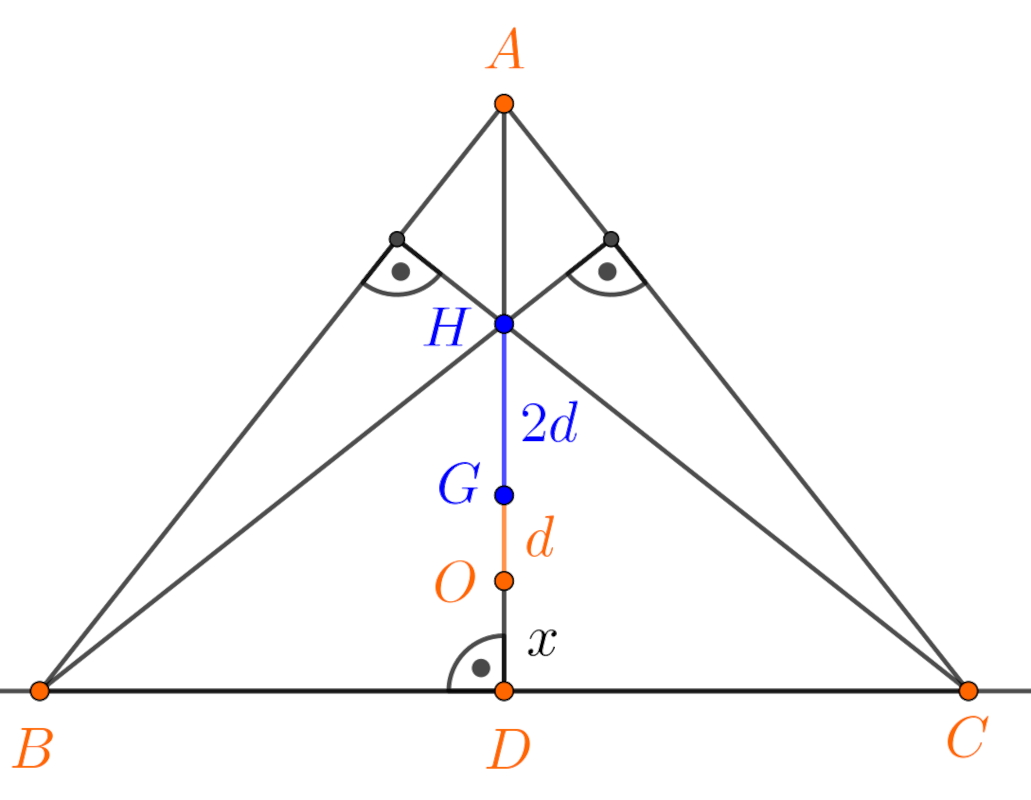
1. ábra
Az \(\displaystyle AD\) súlyvonal \(\displaystyle A\)-tól távolabbi harmadolópontja \(\displaystyle G\), emiatt
\(\displaystyle \displaystyle{\frac{GD}{AG}=\frac{1}{2}},\)
vagyis az ábra jelöléseivel
\(\displaystyle \displaystyle{\frac{x+d}{R-d}=\frac{1}{2}},\)
innen egyszerű átalakítással kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{x=\frac{R-3d}{2}}.\) |
Nyilvánvaló, hogy a feltételeknek csak olyan felvett \(\displaystyle R\) sugár felel meg, amelyre \(\displaystyle x>0\), vagyis amelyre \(\displaystyle R>3d\). Ilyen \(\displaystyle R\) tetszőleges \(\displaystyle d>0\) mellett nyilván létezik.
Az (1) és (2) összefüggések alapján a feltételeknek eleget tevő háromszög megszerkeszthető. Először megszerkesztjük (1) szerint a körülírt kör \(\displaystyle O\) középpontját, majd (2)-nek megfelelően a \(\displaystyle D\) pontot, valamint megrajzoljuk az \(\displaystyle O\) középpontú és \(\displaystyle R\) sugarú kört, ahol \(\displaystyle R\) eleget tesz az \(\displaystyle R>3d\) feltételnek. Ezután a \(\displaystyle D\) pontban merőlegest állítunk a \(\displaystyle DH\) egyenesre, ennek a merőlegesnek és a körülírt körnek a metszéspontjai a háromszög \(\displaystyle B\) és \(\displaystyle C\) csúcsai.
A \(\displaystyle H\) és \(\displaystyle G\) pontokat más módon is felvehetjük (2. ábra).
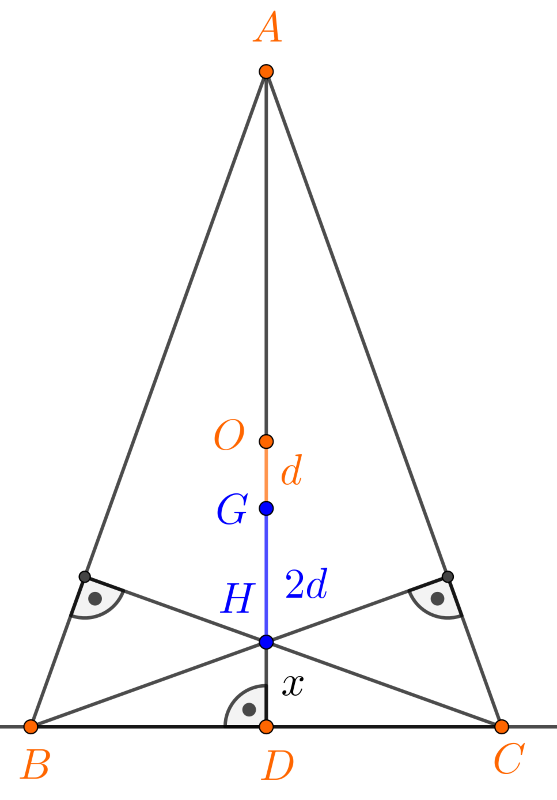
2. ábra
A súlypont azonban most is ugyanúgy harmadolja az \(\displaystyle AD\) súlyvonalat és a \(\displaystyle HO\) szakaszt, ezért (1) és (2) most is érvényben marad, tehát a szerkesztés módja sem változik.
A szerkesztés eredménye ugyanakkor nem egyértelmű, hiszen az \(\displaystyle R>3d\) egyenlőtlenségnek végtelen sok \(\displaystyle R\) tesz eleget, de minden ennek megfelelően szerkesztett háromszög egyenlő szárú és hegyesszögű, magasságpontja \(\displaystyle H\), súlypontja \(\displaystyle G\).
Ezzel a megoldást befejeztük.
Statisztika:
A KöMaL 2025. novemberi matematika feladatai

