 |
A C. 1877. feladat (2025. november) |
C. 1877. Az \(\displaystyle ABC\) hegyesszögű háromszög körülírt körén az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) pontot nem tartalmazó \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) ív felezőpontja rendre \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\). A \(\displaystyle DE\) szakasz a \(\displaystyle BC\), illetve \(\displaystyle CA\) oldalakat a \(\displaystyle P\), illetve \(\displaystyle Q\) pontban, az \(\displaystyle EF\) szakasz a \(\displaystyle CA\), illetve \(\displaystyle AB\) oldalakat az \(\displaystyle R\), illetve \(\displaystyle S\) pontban, végül az \(\displaystyle FD\) szakasz az \(\displaystyle AB\), illetve \(\displaystyle BC\) oldalakat a \(\displaystyle T\), illetve \(\displaystyle U\) pontban metszi. Bizonyítsuk be, hogy a \(\displaystyle PRT\) és \(\displaystyle QSU\) háromszögek területe egyenlő.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2025. december 10-én LEJÁRT.
Megoldás. Mivel az \(\displaystyle ABC\) háromszög körülírt körében azonos hosszúságú ívekhez azonos nagyságú kerületi szögek tartoznak, ezért \(\displaystyle AD, BE, CF\) rendre felezi a \(\displaystyle CAB\sphericalangle=\alpha, ABC\sphericalangle=\beta, BCA\sphericalangle=\gamma\) szöget, illetve az \(\displaystyle AD, BE, CF\) egyenesek közös pontja a háromszög beírt körének \(\displaystyle I\) középpontja.
Először azt fogjuk bizonyítani, hogy \(\displaystyle TQ\parallel BC\), ezért a \(\displaystyle T\), illetve \(\displaystyle Q\) pontokat külön-külön összekötjük az \(\displaystyle I\) ponttal. Tekintsük a következő ábrát.
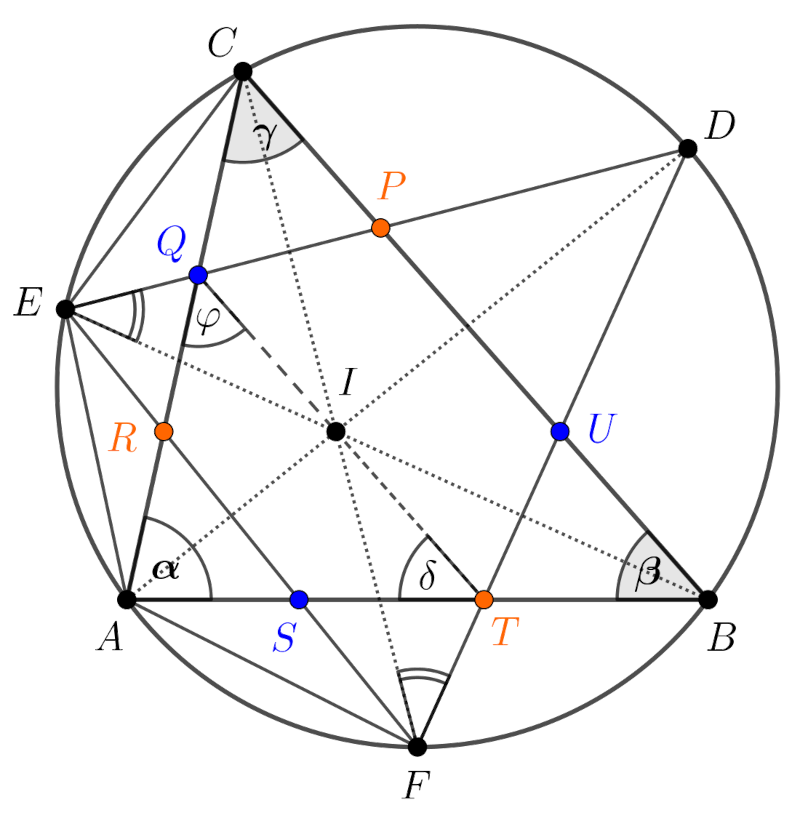
1. ábra
Mivel \(\displaystyle AD\) felezi a \(\displaystyle CAB\sphericalangle=\alpha\) szöget, ezért \(\displaystyle \displaystyle{CAD\sphericalangle=DAB\sphericalangle=\frac{\alpha}{2}}\), ebből a kerületi szögek tétele alapján kapjuk, hogy
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{DEB\sphericalangle=CFD\sphericalangle=\frac{\alpha}{2}}.\) |
Az (1) összefüggés azt jelenti, hogy a \(\displaystyle TI\) egyenes ugyanazon oldalán fekvő \(\displaystyle A\) és \(\displaystyle F\) pontból a \(\displaystyle TI\) szakasz \(\displaystyle \displaystyle{\frac{\alpha}{2}}\) nagyságú szögben látszik, tehát \(\displaystyle AFTI\) húrnégyszög, illetve a \(\displaystyle QI\) egyenes azonos oldalán levő \(\displaystyle A\) és \(\displaystyle E\) pontból a \(\displaystyle QI\) szakasz is \(\displaystyle \displaystyle{\frac{\alpha}{2}}\) szögben látszik, emiatt \(\displaystyle AIQE\) szintén húrnégyszög.
Az \(\displaystyle AFTI\) húrnégyszög köré írt körben az \(\displaystyle AI\) egyenes azonos oldalán levő \(\displaystyle T\) és \(\displaystyle F\) pontból az \(\displaystyle AI\) szakasz azonos nagyságú szögben látszik, vagyis \(\displaystyle ATI\sphericalangle=AFI\sphericalangle\), de mivel \(\displaystyle AFI\sphericalangle=AFC\sphericalangle=ABC\sphericalangle=\beta\), ezért \(\displaystyle ATI\sphericalangle=\delta=\beta\).
Ebből az következik, hogy
| \(\displaystyle (2)\) | \(\displaystyle TI\parallel BC.\) |
Az \(\displaystyle AIQE\) húrnégyszög köré írt körben pedig a \(\displaystyle AI\) egyenes azonos oldalán levő \(\displaystyle Q\) és \(\displaystyle E\) pontból az \(\displaystyle AI\) szakasz azonos nagyságú szögben látszik, vagyis \(\displaystyle IQA\sphericalangle=IEA\sphericalangle\), ugyanakkor \(\displaystyle IEA\sphericalangle=BEA\sphericalangle=BCA\sphericalangle=\gamma\), ezért \(\displaystyle IQA\sphericalangle=\varphi=\gamma\), emiatt
| \(\displaystyle (3)\) | \(\displaystyle QI\parallel BC.\) |
A (2) és (3) összefüggések egyszerre csak úgy állhatnak fenn, ha a \(\displaystyle T, I, Q\) pontok egy egyenesen vannak és \(\displaystyle TQ\parallel BC\).
A fentiekhez hasonlóan láthatjuk be, hogy \(\displaystyle PS\parallel CA\), illetve \(\displaystyle RU\parallel AB\), valamint azt, hogy \(\displaystyle PS\) és \(\displaystyle RU\) is átmennek az \(\displaystyle I\) ponton.
Tekintsük most a 2. ábrát, amelyen megjelöltük az \(\displaystyle IUQ\) és \(\displaystyle IPR\) háromszögeket. Igazolni fogjuk, hogy ezek területe egyenlő.

2. ábra
Az \(\displaystyle IUQ\) és \(\displaystyle IPQ\) háromszögek területe egyenlő, mert az \(\displaystyle IQ\) alapjuk közös, az \(\displaystyle U\), illetve \(\displaystyle P\) csúcsaikhoz tartozó magasságuk pedig \(\displaystyle IQ\parallel UP\) miatt egyenlő.
Az \(\displaystyle IPQ\) háromszög területe egyenlő az \(\displaystyle IPR\) háromszög területével, mert az \(\displaystyle IP\) oldaluk, és a \(\displaystyle Q\), valamint \(\displaystyle R\) csúcsaikhoz tartozó magasságuk \(\displaystyle IP\parallel QR\) következtében egyenlő.
Ehhez hasonlóan könnyen bizonyítható, hogy az \(\displaystyle IQS\) és \(\displaystyle IRT\) háromszögek is egyenlő területűek, ahogyan egyenlő a területe az \(\displaystyle ISU\) és \(\displaystyle ITP\) háromszögeknek is.
Eredményeinkből pedig az következik, hogy \(\displaystyle t_{IUQ}+t_{IQS}+t_{ISU}=t_{IPR}+t_{IRT}+t_{ITP}\), azaz
\(\displaystyle t_{QSU}=t_{PRT},\)
ez pedig éppen a bizonyítandó állítás.
Hasonlóképpen járhatunk el, ha az \(\displaystyle ABC\) egyenlő szárú, hegyesszögű háromszög, ebben az esetben a megoldás némileg rövidebb. Ha pedig \(\displaystyle ABC\) szabályos háromszög, akkor a feladat állítása triviális, hiszen könnyen belátható, hogy \(\displaystyle PRT\) és \(\displaystyle QSU\) egybevágó szabályos háromszögek.
Megjegyzések. a) A megoldás alapján könnyen beláthatjuk, hogy \(\displaystyle AD\perp EF, BE\perp FD\) és \(\displaystyle CF\perp DE\), tehát a \(\displaystyle DEF\) háromszög magasságpontja \(\displaystyle I\).
b) A megoldásból egyszerűen következik az is, hogy \(\displaystyle DB=DC=DI\), azaz a \(\displaystyle BCI\) háromszög körülírt körének középpontja \(\displaystyle D\), és hasonlóan láthatjuk be, hogy a \(\displaystyle CAI\), illetve \(\displaystyle ABI\) háromszög körülírt körének középpontja \(\displaystyle E\), illetve \(\displaystyle F\).
Statisztika:
17 dolgozat érkezett. 5 pontot kapott: Bao Nguyen Gia, Budai Máté, Németh Ábel. 4 pontot kapott: Hirmann Dorottya. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2025. novemberi matematika feladatai

