A C. 1881. feladat (2025. december)

C. 1881. Adott egy \(\displaystyle n\times n\)-es sakktábla, melyet szeretnénk lefedni átfedésmentesen 3 négyzetből álló L betűkkel úgy, hogy legfeljebb egy mező maradjon üresen. Mutassuk meg, hogy ez tetszőleges \(\displaystyle n\neq3\) pozitív természetes számra megtehető. (Az L betűk minden oldala rácsvonalra kell, hogy essen.)

Javasolta: Czett Mátyás (Zalaegerszeg)

(5 pont)

A beküldési határidő 2026. január 12-én LEJÁRT.

Megoldás. Először is készítsünk listát arról, hogy milyen téglalapokat tudunk maradéktalanul lefedni L alakú elemekkel viszonylag könnyedén.

• Két elem megfelelő összeillesztésével egy \(\displaystyle 2\times3\)-as téglalap könnyen lefedhető.
• 2 db \(\displaystyle 2\times3\)-as lefedett téglalap felhasználásával készíthető \(\displaystyle 2\times6\)-os, 3 db \(\displaystyle 3\times2\)-es lefedett téglalap egymásra helyezésével pedig \(\displaystyle 3\times6\)-os lefedett téglalap.
• Az előző két téglalapot jól használhatjuk tetszőleges \(\displaystyle 6\times n\)-es téglalap fedésére, ha \(\displaystyle n\geq 2\). Ehhez páros \(\displaystyle n\) esetén \(\displaystyle \frac{n}{2}\) db \(\displaystyle 2\times6\)-os, páratlan \(\displaystyle n\) esetén egy \(\displaystyle 3\times6\)-ost és megfelelő számú (\(\displaystyle \frac{n-3}{2}\) db) \(\displaystyle 2\times 6\)-es téglalapot kell egymás mellé helyeznünk.

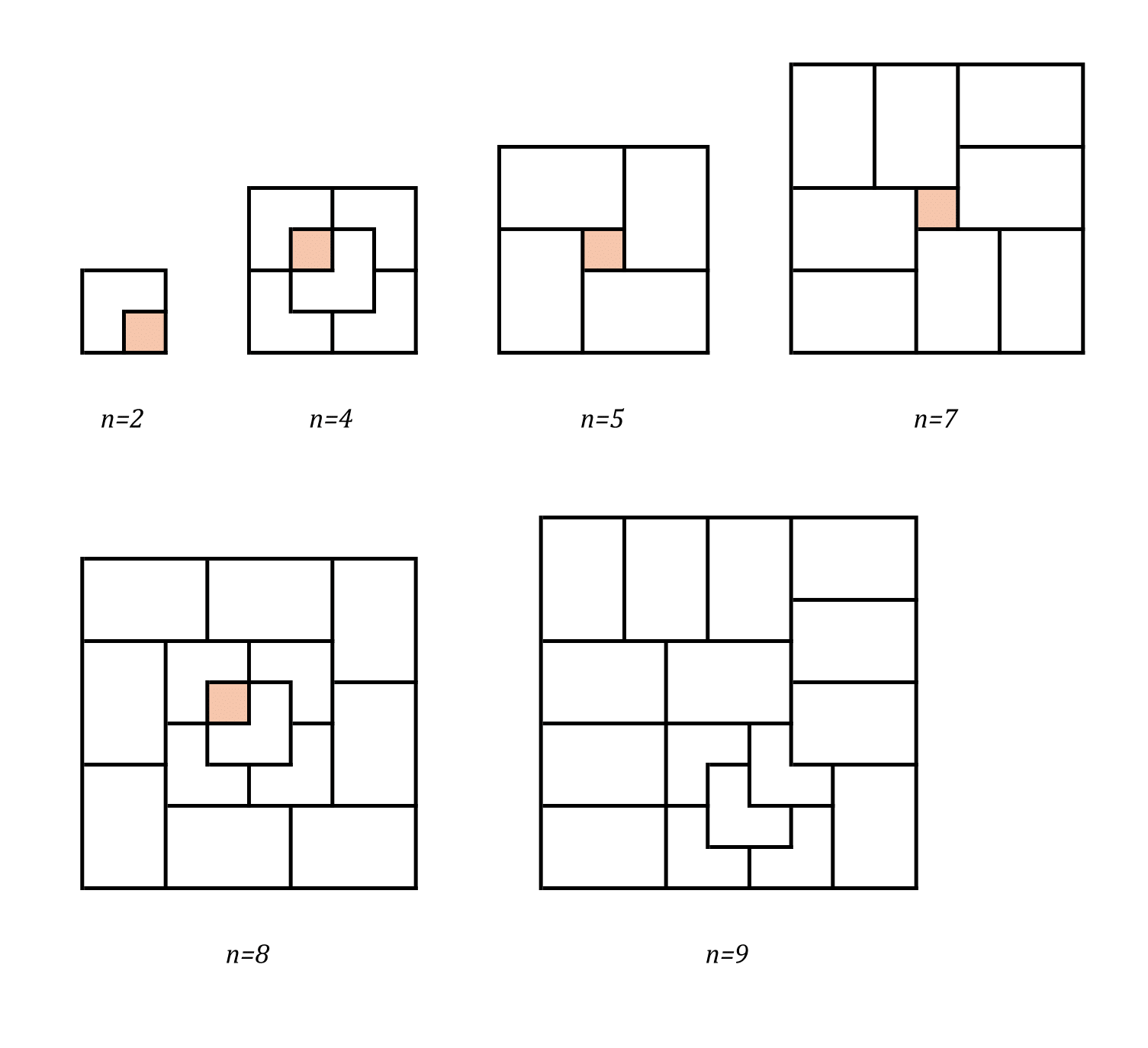
Ezután belátjuk, hogy az \(\displaystyle n\times n\)-es négyzet megfelelő fedése \(\displaystyle n\leq 9\) és \(\displaystyle n\neq 3\) esetén megtehető. Az \(\displaystyle n=1\) esetben sikerrel jártunk anélkül, hogy letettünk volna elemet, az \(\displaystyle n=2, n=4, n=5\) esetet az ábra első sora mutatja. A \(\displaystyle 6\times 6\)-os sakktábla lefedését már láttuk korábban a téglalapok vizsgálatánál, a \(\displaystyle 7\times7\)-es, \(\displaystyle 8 \times 8\)-as és \(\displaystyle 9 \times 9\)-es eset pedig a második sorban látható. Az ábrán a téglalapok \(\displaystyle 2\times 3\)-as táblákat jelölnek, melyek maradéktalan fedését korábban megmutattuk.

A bizonyítás folytatásához szükség van a következő segédállításra:

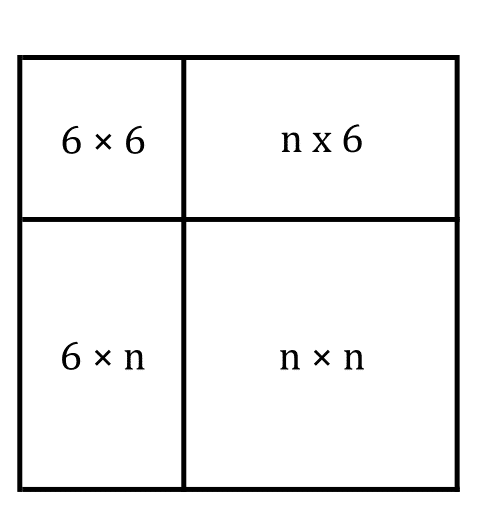
Állítás: Ha az \(\displaystyle n\times n\)-es négyzet megfelelően lefedhető, akkor az \(\displaystyle (n+6) \times (n+6)\)-os négyzet is lefedhető megfelelően.

Bizonyítás: Az \(\displaystyle (n+6) \times (n+6)\)-os négyzet felbontható négy téglalapra a lenti ábrán látható módon, 1 db \(\displaystyle n\times n\)-esre, 2 db \(\displaystyle n\times 6\)-osra és 1 db \(\displaystyle 6\times 6\)-osra. Mivel korábban láttuk, hogy a négy téglalap közül az \(\displaystyle n\times 6\)-osok és a \(\displaystyle 6\times 6\)-os teljesen lefedhetőek L alakú elemekkel, az \(\displaystyle n\times n\)-es pedig az állítás feltevése szerint legfeljebb egy négyzet kihagyásával lefedhető, ezért igaz az állítás. \(\displaystyle \blacksquare\)

A segédállítást felhasználva a feladat állítása teljes indukció segítségével könnyen igazolható. Ha ugyanis egy \(\displaystyle k\) oldalhosszúságú sakktáblát \(\displaystyle (k>9)\) kell lefednünk, először számoljuk ki \(\displaystyle k\) hatos maradékát. Ha a \(\displaystyle k\) hatos maradéka \(\displaystyle 0\), akkor induljunk ki egy \(\displaystyle 6\times 6\)-os tábla lefedéséből, majd a segédállításban látott módon bővítsük ezt \(\displaystyle 12\times 12\)-es lefedéssé, majd \(\displaystyle 18\times 18\)-as lefedéssé, stb. Az eljárást kellő számban megismételgetve megkapjuk egy \(\displaystyle k\times k\)-as tábla megfelelő lefedését.

Más hatos maradékok esetén hasonlóan járhatunk el: ha \(\displaystyle k\) hatos maradék 1, a \(\displaystyle 7\times 7\)-es tábla lefedéséből induljunk ki, és azt bővítgessük, ha a hatos maradék 2, akkor \(\displaystyle 2\times 2\)-esből, ha a maradék 3, akkor \(\displaystyle 9\times9\)-esből, ha a maradék 4, akkor \(\displaystyle 4\times 4\)-esből, ha pedig a maradék 5, akkor \(\displaystyle 5\times 5\)-ösből. A segédállítás felhasználásával így igazoltuk a feladat állítását.

Megjegyzés: Bár a feladat szövege nem kéri, a probléma teljes vizsgálatához hozzátartozik annak bizonyítása, hogy \(\displaystyle n=3\) esetén a lefedés nem megvalósítható. \(\displaystyle 3\times3\)-as tábla esetén teljes fedést kellene létrehoznunk, hisz az L betűkkel fedett mezők száma mindenképpen a 3 többszöröse. Hogy teljes fedés miért nem lehetséges, indirekt igazolható, például esetszétválasztással a jobb alsó sarkot fedő elem elhelyezkedése szerint.

De gondolkodhatunk így is: színezzük a \(\displaystyle 3\times 3\)-as sakktáblát sakktáblaszerűen, a bal felső elem legyen fehér. Mivel így 5 fehér és 4 fekete mező keletkezik, ezért az L betűk közül kettőnek kell 2 fehér mezőt fedni, egynek pedig egyet (3 és 0 fehér mezőt nem tud fedni L betű). Viszont egy L betű csak akkor fedhet 2 fehér mezőt, ha letakarja a középső mezőt is. Ezek szerint megfelelő fedés esetén a középső mezőt két elem is takarná, ami ellentmondás.

Statisztika:

A C. 1881. feladat értékelése még nem fejeződött be.

A KöMaL 2025. decemberi matematika feladatai