 |
A C. 1882. feladat (2025. december) |
C. 1882. Legyen \(\displaystyle ABCD\) konvex négyszög, az \(\displaystyle ABD\) háromszög beírt körének középpontját jelölje \(\displaystyle I\). Mutassuk meg, hogy ha \(\displaystyle CB=CD=CI\), akkor \(\displaystyle ABCD\) húrnégyszög.
Javasolta: Vígh Viktor (Sándorfalva)
(5 pont)
A beküldési határidő 2026. január 12-én LEJÁRT.
Megoldűs. Az \(\displaystyle ABD\) háromszög beírt körének \(\displaystyle I\) középpontja a háromszög belső pontja. Mivel \(\displaystyle ABCD\) konvex négyszög, ezért a \(\displaystyle C\) pont csak a \(\displaystyle DAB\) szögtartomány belső pontja lehet. Tekintsük a következő ábrát.
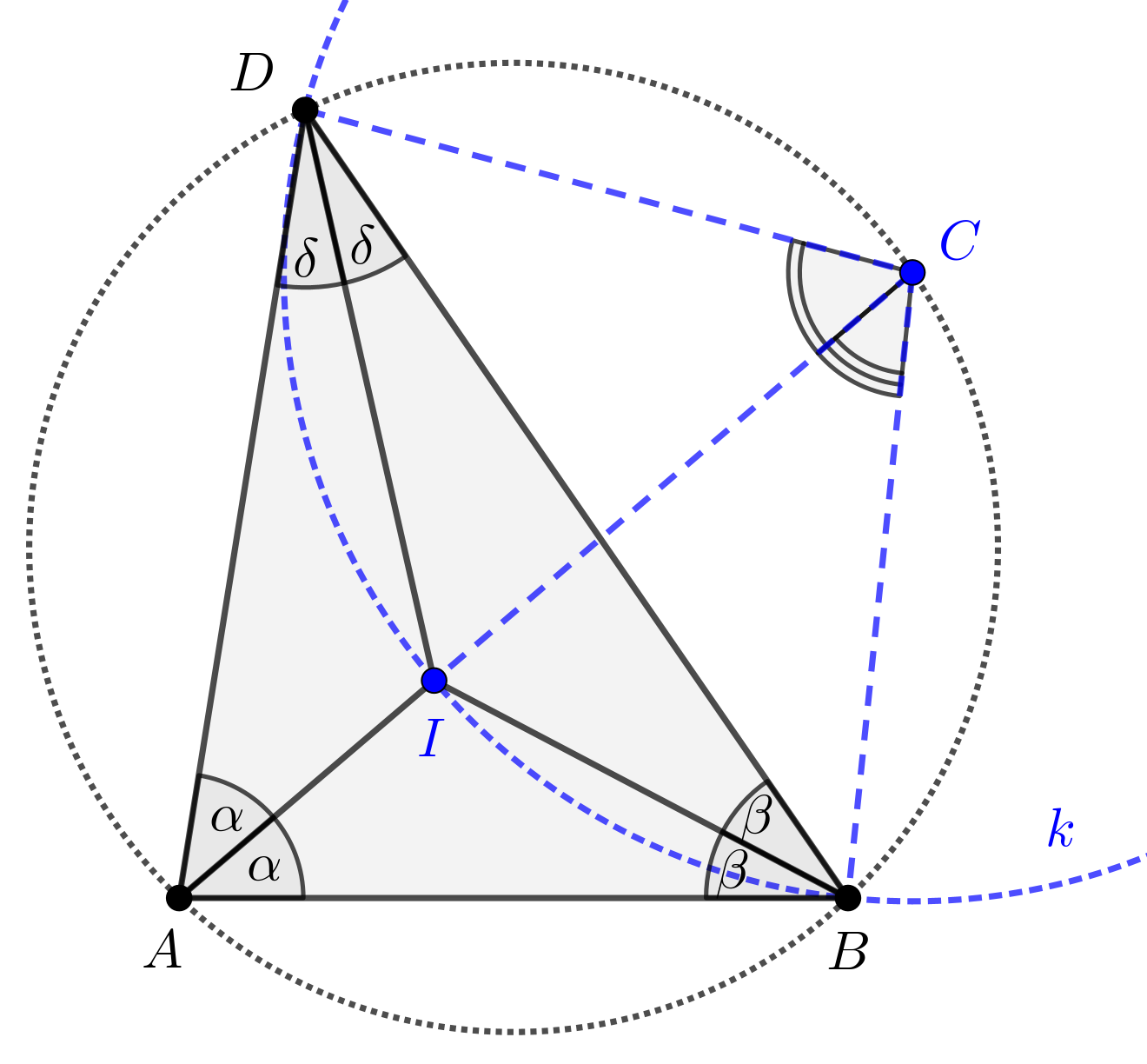
Az \(\displaystyle ABD\) háromszögben \(\displaystyle I\) a belső szögfelezők metszéspontja, ezért az \(\displaystyle IAB\sphericalangle=\alpha; IBD\sphericalangle=\beta; IDA\sphericalangle=\delta\) jelöléssel kapjuk, hogy a háromszög belső szögeinek összege
| \(\displaystyle (1)\) | \(\displaystyle 2\alpha+2\beta+2\gamma=180^{\circ}.\) |
A \(\displaystyle CB=CD=CI\) feltételből következik, hogy a \(\displaystyle BDI\) háromszög \(\displaystyle k\) körülírt körének középpontja éppen \(\displaystyle C\). Ezért a \(\displaystyle k\) körben a \(\displaystyle B\) pontot nem tartalmazó \(\displaystyle DI\) ívhez \(\displaystyle \beta\), a \(\displaystyle D\) pontot nem tartalmazó \(\displaystyle BI\) ívhez pedig \(\displaystyle \delta\) nagyságú kerületi szög tartozik.
A kerületi és középponti szögek összefüggése alapján ebből azt kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle ICD\sphericalangle=2\beta,\quad BCI\sphericalangle=2\delta.\) |
A (2) összefüggésből adódik, hogy az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle A\) és \(\displaystyle C\) csúcsánál levő belső szögek összege \(\displaystyle DAB\sphericalangle+BCD\sphericalangle=2\alpha+2\beta+2\gamma\), ez pedig (1) alapján azt jelenti, hogy az \(\displaystyle ABCD\) négyszög két szemközti szögének összege \(\displaystyle 180^{\circ}\).
Ebből a húrnégyszögek tételének megfordítása alapján következik, hogy \(\displaystyle ABCD\) valóban húrnégyszög.
Ezzel a feladat állítását igazoltuk.
Megjegyzés. A feladat állításának igazolásához felhasználhattuk volna azt a jól ismert tételt (lásd például: Geometriai feladatok gyűjteménye I. kötet, 967. feladat), amely szerint a \(\displaystyle BDI\) kör középpontja az \(\displaystyle ABD\) kör \(\displaystyle BD\) ívének felezőpontja, ez jelen esetben éppen a \(\displaystyle C\) pont.
Statisztika:
A C. 1882. feladat értékelése még nem fejeződött be.
A KöMaL 2025. decemberi matematika feladatai

