Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

A C. 907. feladat (2007. szeptember)

C. 907. Az a oldalú ABCD, és a b oldalú BEFG négyzeteket az ábrán látható módon rajzoltuk egymás mellé.

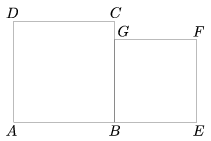
Fejezzük ki a-val és b-vel az AB, BE, FC és DG szakaszok felezőpontjai által meghatározott négyszög területét.

(5 pont)

A beküldési határidő 2007. október 15-én LEJÁRT.

Megoldás: F₁F₄ az ABGD trapéz középvonala, így párhuzamos AD-vel, és hossza $\frac{AD+BG}{2}=\frac{a+b}{2}$ .

F₂F₃ az EFCB trapéz középvonala, így párhuzamos BC-vel, hossza pedig $\frac{BC+EF}{2}=\frac{a+b}{2}$ .

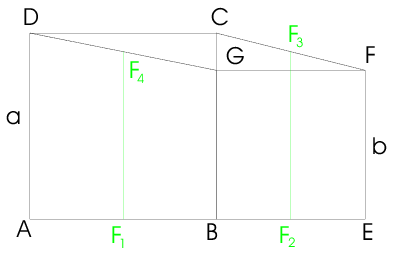
Mivel AD||BC, ezért F₁F₂F₃F₄ két szemben fekvő oldala, F₁F₄ és F₂F₃ párhuzamos és egyenlő, tehát ez a négyszög paralelogramma. Mivel oldalai merőlegesek egymásra ( $F_1F_4||AD\perp AE$ ), ezért téglalap.

F₁F₂=F₁B+BF₂=a/2+b/2, tehát F₁F₂F₃F₄ négyzet. Így területe:

$T=\left(\frac{a+b}{2}\right)^2.$

Statisztika:

617 dolgozat érkezett.

5 pontot kapott: 168 versenyző.

4 pontot kapott: 84 versenyző.

3 pontot kapott: 71 versenyző.

2 pontot kapott: 84 versenyző.

1 pontot kapott: 69 versenyző.

0 pontot kapott: 131 versenyző.

Nem versenyszerű: 10 dolgozat.

A KöMaL 2007. szeptemberi matematika feladatai

617 dolgozat érkezett.
5 pontot kapott:	168 versenyző.
4 pontot kapott:	84 versenyző.
3 pontot kapott:	71 versenyző.
2 pontot kapott:	84 versenyző.
1 pontot kapott:	69 versenyző.
0 pontot kapott:	131 versenyző.
Nem versenyszerű:	10 dolgozat.