 |
A C. 923. feladat (2007. december) |
C. 923. Egy húrtrapéz párhuzamos oldalai a=10, c=15 hosszúak, köré írható körének sugara r=10. Mekkorák lehetnek a szárai? Mekkora a területe?
(5 pont)
A beküldési határidő 2008. január 15-én LEJÁRT.
Megoldás. Két ilyen trapéz is van. Az egyik tartalmazza a kör középpontját, a másik nem.
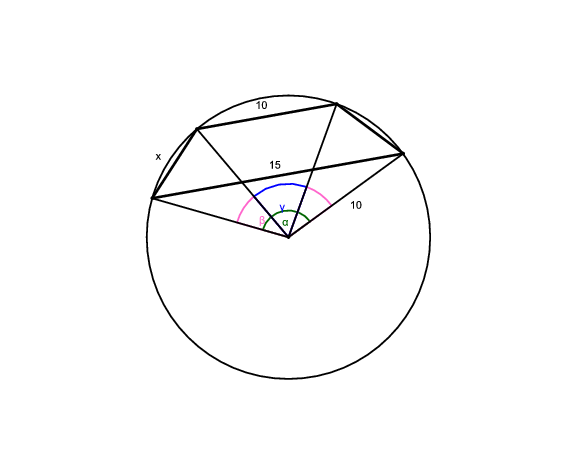
Az adatok alaján  =60o, hiszen egyenlő oldalú háromszög egyik szöge.
=60o, hiszen egyenlő oldalú háromszög egyik szöge.
Felírható még, hogy , amiből
 /2
/2 48,59o és
48,59o és 
 97,18o.
97,18o.
Ebből kiszámoljuk  -t:
-t: .
Ezt felhasználva: miatt
.
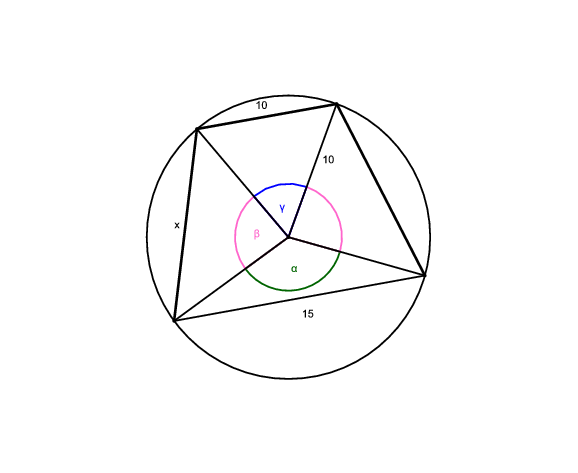
Ekkor  és
és  ugyannyi, mint az előbb, csak
ugyannyi, mint az előbb, csak  lesz más:
lesz más:
Innen miatt x2=20sin (101,41o/2)
 15,48.
15,48.
A két terület:
Statisztika:
322 dolgozat érkezett. 5 pontot kapott: 128 versenyző. 4 pontot kapott: 49 versenyző. 3 pontot kapott: 89 versenyző. 2 pontot kapott: 30 versenyző. 1 pontot kapott: 15 versenyző. 0 pontot kapott: 8 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2007. decemberi matematika feladatai
