A G. 603. feladat (2017. május)

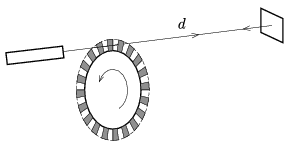
G. 603. Gondosan megmunkált, fogazott korongot forgatva a fogak közötti hézagon áthaladó vékony lézersugár útját szaggatjuk meg, amely a korongtól \(\displaystyle d=1000\) m-re elhelyezett tükörről úgy verődik vissza, hogy ugyanazon a hézagon érkezik a kiindulási helyére. A nyugalomból induló korong fordulatszáma egyenletesen növekszik, és 1 perccel az indítás után éri el a másodpercenkénti 600-as értéket. Az indítástól számítva mennyi idő múlva tűnik el a visszavert fénysugár a korong fényforrásos oldalán? A korong peremén 300 fog van, a fogak és a rések mérete megegyezik.

(3 pont)

A beküldési határidő 2017. június 12-én LEJÁRT.

Megoldás. A fény sebessége \(\displaystyle 300\,000\) km/s, tehát a tükörig és vissza összesen

\(\displaystyle \Delta t= \frac{2\cdot 1000~\rm m}{300\,000~\rm km/s}=6{,}67\cdot10^{-6}~\rm s\)

idő alatt jut el a fény. Ha ezalatt a korong egy fognyit (a teljes kör 1/600-ad részét) fordul el, a visszaérkező fénysugár már nem juthat át a fogak között. Ez akkor következik be, amikor a korong körülfordulási ideje

\(\displaystyle T=600\cdot \Delta t=0{,}004~\rm s,\)

vagyis a fordulatszáma: \(\displaystyle f=1/T=250~1/\rm s\). Ezt a forgási sebességet az indítástól számított 25 másodperc múlva éri el az egyre gyorsabban forgó korong.

Statisztika:

16 dolgozat érkezett.
3 pontot kapott:	Békési Péter, Fekete András Albert, Fialovszky Márk, Geretovszky Anna, Kozák 023 Áron, Merkl Levente, Pácsonyi Péter, Rusvai Miklós, Šárai Krisztina, Szakáll Lili, Tanner Norman, Urszuly Csenge.
2 pontot kapott:	Bonifert Balázs, Földesi András, Horváth 999 Anikó.
1 pontot kapott:	1 versenyző.

A KöMaL 2017. májusi fizika feladatai