 |
A G. 720. feladat (2020. október) |
G. 720. A Tour de France kerékpáros körversenyen a versenyzők vízszintes terepen egyenletesen, 50 km/h sebességgel haladnak. A ,,mezőny'' és a ,,szökevények'' közötti távolság 1 km. Amikor egy enyhe, 5 km hosszú emelkedőhöz érnek, a sebességük nagyon hamar 40 km/h-ra csökken, majd az ugyancsak 5 km hosszú ereszkedőn nagyon hamar 60 km/h-ra nő. Ábrázoljuk, hogyan változik a mezőny és a szökevények közötti távolság az idő függvényében attól az időponttól kezdve, amikor a szökevények elérik az emelkedő alját!
Közli: Szabó Endre, Vágfüzes (Szlovákia)
(4 pont)
A beküldési határidő 2020. november 16-án LEJÁRT.
Megoldás. Válasszuk az időmérés kezdőpontjának azt az időpontot, amikor a szökevények elérik az emelkedő alját. A mezőny
\(\displaystyle t_1=\frac{1~\rm km}{50~\frac{\rm km}{\rm h}}=\frac{1}{50}~\text{óra}=1{,}2~\text{perc}\)
múlva ér ugyanehhez a ponthoz.
A szökevények
\(\displaystyle t_2=\frac{5~\rm km}{40~\frac{\rm km}{\rm h}}=\frac{1}{8}~\text{óra}=7{,}5~\text{perc}\)
időpontban érnek az emelkedő tetejére, a mezőny 1,2 perccel később, tehát \(\displaystyle t_3=8{,}7\) perckor ér ugyanoda.
A szökevények
\(\displaystyle t_\text{lefelé}=\frac{5~\rm km}{60~\frac{\rm km}{\rm h}}=\frac{1}{12}~\text{óra}=5~\text{perc}\)
idő alatt gurulnak le a lejtő aljáig, tehát \(\displaystyle t_4=12{,}5~\)perckor érnek oda. Őket 1,2 perccel lemaradva követi a mezőny, tehát ők \(\displaystyle t_5=\)13,7 perckor érnek le. Ettől kezdve a szökevények is és a mezőny is egyenletesen, 5 km/h sebességgel halad.
A szökevények és a mezőny út-idő grafikonját az 1. ábra mutatja. A mezőny grafikonja a szökevényekéből úgy kapható meg, ha azt a \(\displaystyle t\) tengely irányában 1,2 perccel eltoljuk, hiszen a pálya mentén (bárhol) álló néző az előtte elhaladó két csoport között 1,2 perc időkülönbséget észlel.
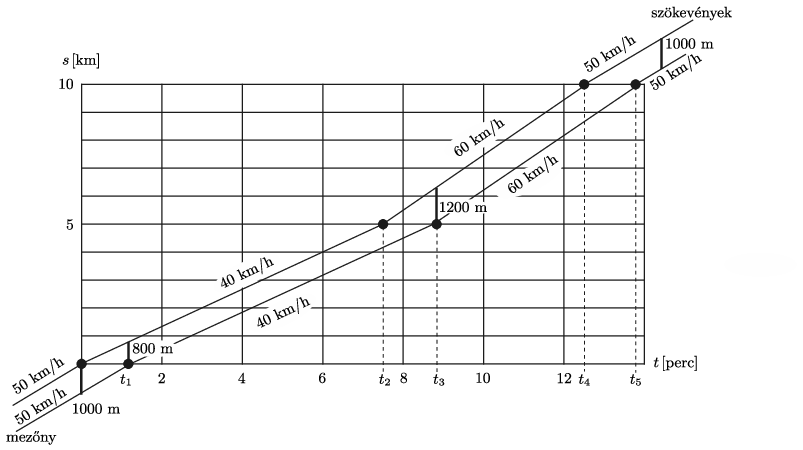
1. ábra
A két csoport közötti távolság \(\displaystyle t\le 0\) esetén (a feladat szövege szerint) \(\displaystyle \Delta s=1\) km. \(\displaystyle t_1\) idő alatt ez a távolság (az állandó, 10 km/h nagyságú sebességkülönbség miatt) egyenletes ütemben
\(\displaystyle 1000~{\rm m}- 10~\frac{\rm km}{\rm h}\cdot 1{,}2~{\rm min}=800~\rm m\)
értékre csökken.
\(\displaystyle t_1\) és \(\displaystyle t_2\) között a két csoport egyforma sebessége miatt a távolságuk nem változik, mindvégig 800 m marad.
\(\displaystyle t_2\) és \(\displaystyle t_3\) között a relatív sebesség 20 km/h, így a csoportok közötti távolság \(\displaystyle 20~\frac{\rm km}{\rm h}\cdot 1{,}2~{\rm min}=400~\rm m\)-rel nő, vagyis 1200 m-re nő.
\(\displaystyle t_3\) és \(\displaystyle t_4\) között a két csoport egyforma sebessége miatt a távolságuk nem változik, mindvégig 1200 m marad.
\(\displaystyle t_4\) és \(\displaystyle t_5\) között a relatív sebesség \(\displaystyle -10\) km/h, így a csoportok közötti távolság \(\displaystyle 10~\frac{\rm km}{\rm h}\cdot 1{,}2~{\rm min}=200~\rm m\)-rel csökken, vagyis 1000 m lesz, és ez a távolság a továbbiakban már nem változik.
Az időben változó \(\displaystyle \Delta s(t)\) távolságot a 2. ábra mutatja.
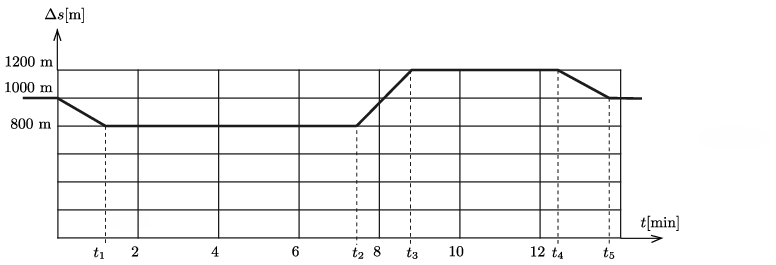
2. ábra
Statisztika:
52 dolgozat érkezett. 4 pontot kapott: Bencz Benedek, Bogdán Benedek, Bruder László, Buzási-Temesi Imre, Cynolter Dorottya, Dancsák Dénes, Emődi Marcell, Fehérvári Donát, Havasi Marcell Milán, Koczkás Árpád, Kohut Márk Balázs, Kolláth Gergely Sándor, Kovács Dorina , Láng Erik, Marozsi Lenke Sára, Medveczki Gábor József, Molnár Kristóf, Morvai Eliza, Novák Péter, Országh Júlia, Schmercz Blanka, Schneider Dávid, Sebestyén József Tas, Stein Felix, Szabó Réka, Szanyi Attila, Szeibert Dominik, Vágó Botond, Veszprémi Rebeka Barbara, Vig Zsófia, Vincze Farkas Csongor, Wórum Soma. 3 pontot kapott: Biszak Ákos, Móricz Benjámin, Patricia Janecsko, Richlik Márton, Sepsei Gréta. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 7 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2020. októberi fizika feladatai

