 |
A G. 760. feladat (2021. november) |
G. 760. Alumíniumból készült, 10 cm magas, kúp alakú testet a csúcsához rögzített fonál segítségével lassan kiemelünk egy téglatest alakú akváriumból. Kezdetben a kúp a 10 cm átmérőjű alapkörén áll az akvárium alján, és a víz teljesen ellepi. Az akvárium térfogata sokkal nagyobb, mint az alumíniumkúpé.
Ábrázoljuk a fonalat feszítő erőt a kúp elmozdulásának függvényében!
A KöMaL Nyári Tábor mérési feladata nyomán
(4 pont)
A beküldési határidő 2021. december 15-én LEJÁRT.
Megoldás. Az \(\displaystyle r\) alapkör-sugarú, \(\displaystyle h\) magas kúp térfogata
\(\displaystyle V_0=\frac{1}{3}r^2\pi h=0{,}26~\rm dm^3,\)
súlya levegőben
\(\displaystyle G_0=V_0\varrho_\text{Al}=6{,}9~\rm N,\)
vízben pedig
\(\displaystyle G_1=G_0\left(1-\frac{\varrho_\text{víz}}{\varrho_\text{Al}}\right)=4{,}3~\rm N.\)
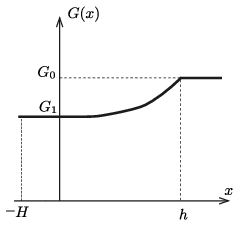
Jelöljük a kúp elmozdulását \(\displaystyle x\)-szel, és legyen \(\displaystyle x=0\) az a helyzet, amikor a kúp csúcsa éppen a vízfelszínnél van. (Ha kezdetben a víz \(\displaystyle H\) magasan ellepte a kúpot, akkor \(\displaystyle x\ge -H\).) A fonalat feszítő erő \(\displaystyle x\) függvényében
\(\displaystyle G(x)\equiv G_1, \qquad \text{ha}~-H<x<0,\)
\(\displaystyle G(x)\equiv G_0, \qquad \text{ha}~ x>h,\)
és
\(\displaystyle G(x)\equiv G_1+\frac{x^3}{h^3}\left(G_0-G_1\right).\)
Kihasználtuk, hogy az eredeti kúphoz hasonló, de csak \(\displaystyle x\) magasságú kúp térfogata \(\displaystyle \frac{x^3}{h^3}V_0.\)
Statisztika:
25 dolgozat érkezett. 4 pontot kapott: Beke Botond, Bocor Gergely, Hruby Laura, Kovács Klára, Sütő Áron. 3 pontot kapott: Heisz András Botond, Jacsman Vencel , Kiss 668 Benedek, Kiss 987 Barnabás, Marosi Botond Máté, Medgyesi Júlia, Richlik Márton, Sós Ádám, Zsova Levente. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2021. novemberi fizika feladatai
