A G. 875. feladat (2025. január)

G. 875. Amikor egy egyenes vonalzót a végétől \(\displaystyle 15\) cm-re támasztunk alá, akkor a vonalzó a végétől \(\displaystyle 5\) cm-re elhelyezett két egyforma pénzérmével egyensúlyozható ki. Amikor az alátámasztást a végétől \(\displaystyle 10\) cm-re helyezzük el, akkor az előbbi helyen \(\displaystyle 6\) pénzérmére van szükség a kiegyensúlyozáshoz. Milyen hosszú a vonalzó?

(4 pont)

A beküldési határidő 2025. február 17-én LEJÁRT.

Megoldás. Az ábrán láthatjuk a kétféle egyensúlyi elrendezést. A pénzérmék súlyát tekintsük egységnyinek, a vonalzó súlya pedig \(\displaystyle G\) egységnek felel meg. Az alátámasztás és a vonalzó súlypontja közötti kezdeti távolságot jelöljük \(\displaystyle x\)-szel, ami a második esetben \(\displaystyle x+5\,\mathrm{cm}\)-re növekszik.

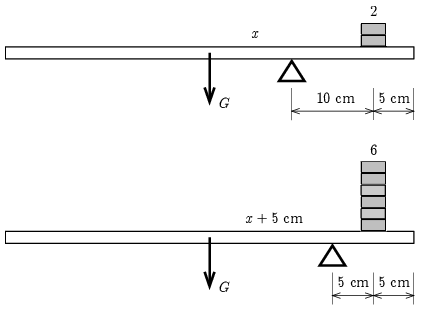
A következő forgatónyomaték egyenleteket írhatjuk fel az alátámasztásra vonatkozóan:

\(\displaystyle Gx=2\,\cdot\,10\,\mathrm{cm}\)

\(\displaystyle G(x+5\,\mathrm{cm})=6\,\cdot\,5\,\mathrm{cm}\)

Az egyenletek megoldása \(\displaystyle G=2\) egységre és \(\displaystyle x=10\,\mathrm{cm}\)-re vezet. Az ábra alapján leolvashatjuk, hogy a vonalzó 50 cm hosszú.

Statisztika:

41 dolgozat érkezett.
4 pontot kapott:	Békési Máté, Csáki Anikó, Csonka Áron, Gáti Benjamin, Hegedüs Márk, Hollósi Dominik, József Áron, Kiss Lukács Dániel, Kossár Benedek Balázs, Kovács Artúr-Lehel, Kovács Tamás , Lakatos Levente, Medgyesi András, Molnár Sámuel , Nemes Máté Imre, Németh Ábel, Patócs 420 Péter, Rácz Koppány Bendeguz, Sipeki Andor, Sipos Dániel Sándor, Sógor-Jász Soma, Szabó András, Szighardt Anna, Szilaj Petra, Szűcs Kitti, Tóth Domonkos, Vincze Blanka Anna, Vízhányó Janka.
3 pontot kapott:	Horváth Zsombor, Majer Veronika.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2025. januári fizika feladatai