Problem G. 880. (February 2025)

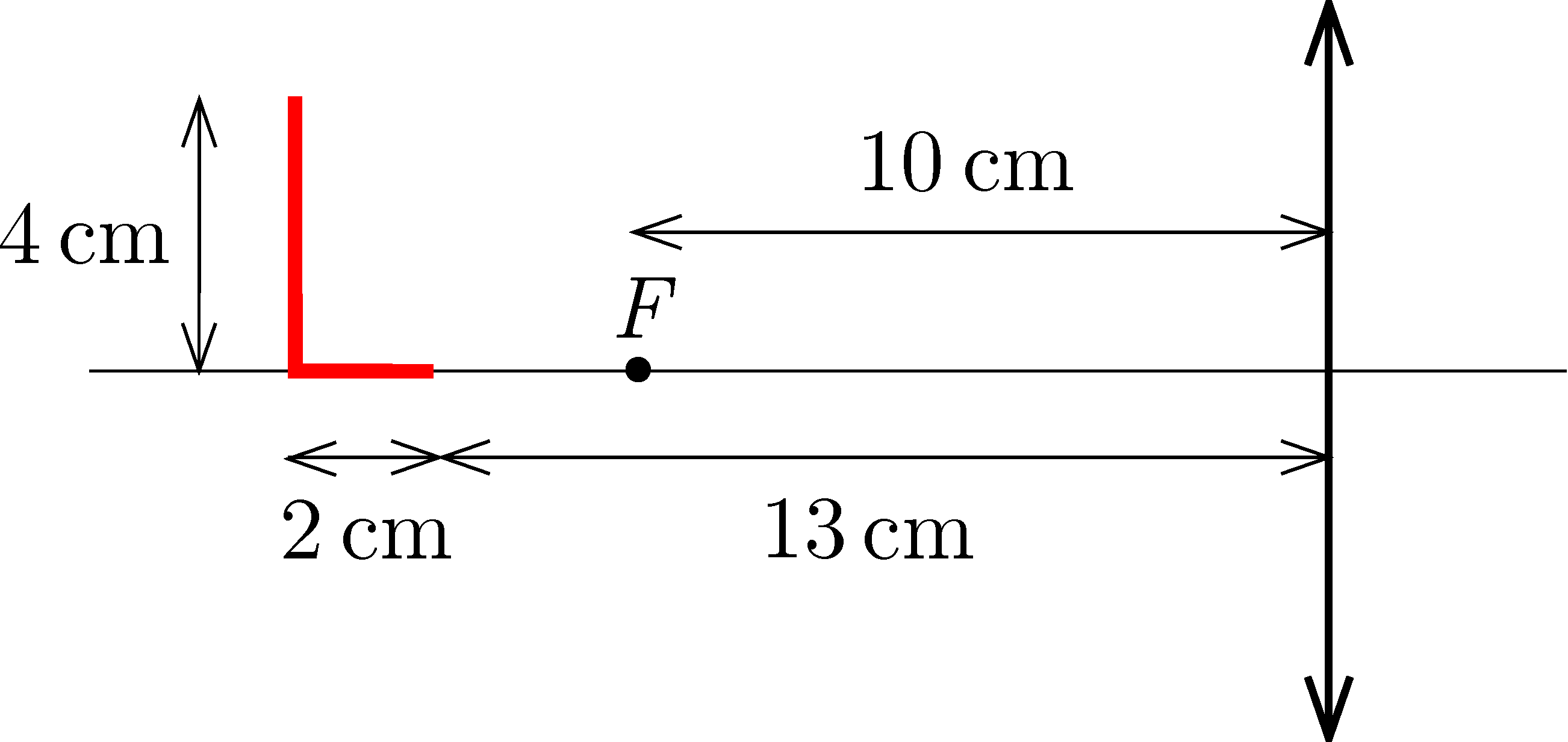
G. 880. An L-shaped luminous LED strip is mounted on the principal axis of a thin converging lens of focal length 10 cm. The longer, 4 cm long leg of the L-shape is perpendicular to the principal axis, and the shorter, 2 cm long leg is aligned with the principal axis such that its end point is \(\displaystyle 13~\mathrm{cm}\) away from the lens, as shown in the figure.

a) Construct the schematic image of the LED strip formed by the lens.

b) Calculate the length of the two parts of the image of the LED strip, the one which is parallel and the other which is perpendicular to the principal axis of the lens. What is the magnification of these parts?

(4 pont)

Deadline expired on March 17, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. a) Ismert, hogy a lencsék egyenest egyenesbe képeznek le, aminek speciális esete, hogy az optikai tengelyen fekvő szakasz képe az optikai tengelyen lesz, továbbá az optikai tengelyre merőleges szakasz képe merőleges lesz az optikai tengelyre. Ennek felhasználásával elegendő megszerkesztenünk az L-alak két végpontjának képét, amint az a következő ábrán látható.

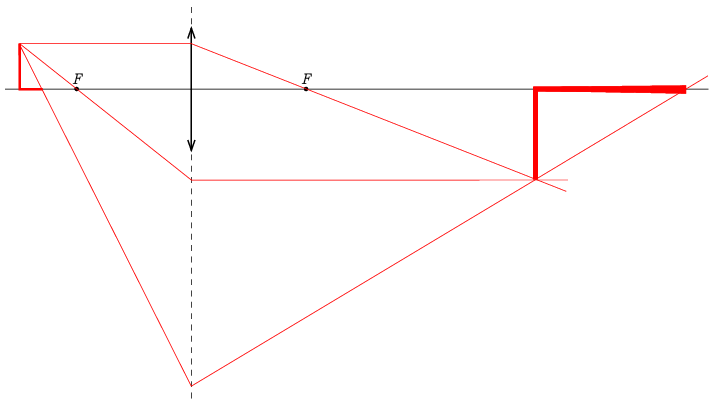
Az L-alak legfelső pontját a szokásos módon, két speciális fénysugár segítségével szerkeszthetjük meg. (Az egyik sugár az optikai tengellyel párhuzamos, a másik pedig átmegy a tárgyoldali fókuszon.) Az L-alak alsó szárának végpontját úgy kaphatjuk meg, hogy egy olyan fénysugarat választunk, amely a függőleges szár tetőpontjából indul, és áthalad az alsó szár végpontján. A fénysugár a lencse síkjánál úgy törik meg, hogy utána áthaladjon a felső pont képén, majd metszi az optikai tengelyt, és ez a metszéspont lesz az alsó szár végpontjának a képe. (Ha egy fénysugár nem halad át ténylegesen a lencsén – annak véges mérete miatt –, a szerkesztés szempontjából akkor is úgy tekinthetjük, mintha áthaladna rajta.)

b) Elegendő az alsó szár két végpontjának a képtávolságát kiszámítani a leképezési törvény segítségével. Kezdjük az L sarkával:

\(\displaystyle \frac{1}{f}=\frac{1}{t}+\frac{1}{k}\qquad\Rightarrow\qquad\frac{1}{10\,\mathrm{cm}}=\frac{1}{15\,\mathrm{cm}}+\frac{1}{k}\qquad\Rightarrow\qquad k=30\,\mathrm{cm}.\)

Látszik, hogy az L-alak függőleges szárának nagyítása kétszeres, tehát a függőleges szár képének hossza 8 cm.

Folytassuk az L-alak vízszintes szakaszának elülső végével:

\(\displaystyle \frac{1}{f}=\frac{1}{t'}+\frac{1}{k'}\qquad\Rightarrow\qquad\frac{1}{10\,\mathrm{cm}}=\frac{1}{13\,\mathrm{cm}}+\frac{1}{k'}\qquad\Rightarrow\qquad k'=\frac{130}{3}\,\mathrm{cm}=43{,}3\,\mathrm{cm}.\)

A vízszintes szakasz képe egy fokozatosan vastagodó tartomány lesz, amelynek hossza: \(\displaystyle k'-k=\tfrac{40}{3}\,\mathrm{cm}=13{,}3\,\mathrm{cm}\), tehát ennek nagyítása \(\displaystyle \tfrac{20}{3}=6{,}67.\)

Statistics:

28 students sent a solution.
4 points:	Csáki Anikó, Hegedüs Márk, Kovács Tamás , Patócs 420 Péter, Rácz Koppány Bendeguz, Vincze Blanka Anna.
3 points:	Békési Máté, Csonka Áron, Horváth Zsombor, József Áron, Lakatos Levente, Macskássy Márk, Nemes Máté Imre, Németh Ábel, Sipeki Andor, Sógor-Jász Soma, Szabó András, Szighardt Anna.
2 points:	6 students.
1 point:	1 student.
0 point:	1 student.

Problems in Physics of KöMaL, February 2025