 |
A G. 893. feladat (2025. szeptember) |
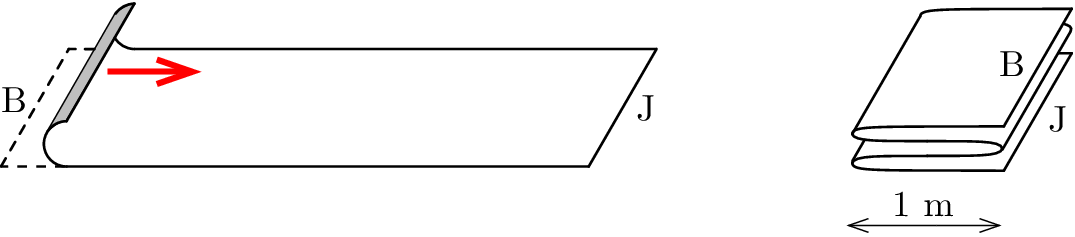
G. 893. A folyosó padlójára leterített, 4 m hosszúságú szőnyeget négyrét (négy egyforma rétegben) összehajtjuk úgy, hogy bal oldali szegélyét (B) megfogjuk, és folyamatosan 20 cm/s nagyságú, vízszintes irányú sebességgel először jobbra, azután balra, majd ismét jobbra visszük. (Lásd az ábrát!)
a) Mennyi időt vesz igénybe a szőnyeg összehajtása?
b) Az összehajtás megkezdésétől mért 5 s elteltével a szőnyegnek milyen hosszú darabja rendelkezik jobbra irányuló sebességgel? A szőnyeg vékony, könnyen hajtható anyagból készült, és nem csúszik meg a padlón. Az irányváltoztatások pillanatszerűen következnek be.
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
A beküldési határidő 2025. október 15-én LEJÁRT.
Megoldás. a) Az egyes hajtogatási lépések alatt megtett utakat az ábra mutatja. A szaggatott vonal a lépés előtti, a folytonos vonal pedig a lépés utáni állapotot ábrázolja.
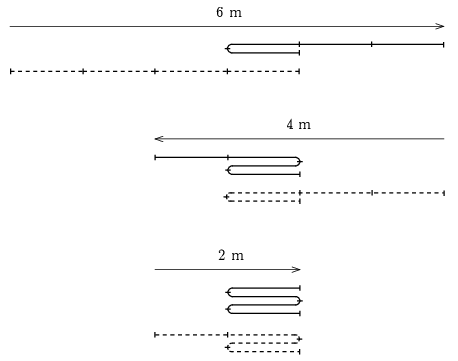
Láthatjuk, hogy összesen \(\displaystyle 6\,\mathrm{m}+4\,\mathrm{m}+2\,\mathrm{m}=12\,\mathrm{m}\) utat kell megtennünk. Mivel 5 s alatt teszünk meg 1 métert, így 60 s, azaz 1 perc kell a szőnyeg összehajtogatásához.
b) Az ábráról azt is leolvashatjuk, hogy amikor a szőnyeg végét valamekkora sebességgel mozgatjuk, akkor a hajtás éppen feleakkora sebességgel mozog. Ha tehát 5 s alatt a szőnyeg vége 1 m-t mozdult el, akkor a hajtás csak 0,5 m-t. Ennek megfelelően ebben a pillanatban a szőnyegnek csak a bal oldali 0,5 m-es darabja mozog 20 cm⁄s nagyságú sebességgel.
Statisztika:
A KöMaL 2025. szeptemberi fizika feladatai

