 |
A G. 894. feladat (2025. szeptember) |
G. 894. Egy \(\displaystyle a\) oldalú, homogén tömegeloszlású, szabályos hatszög alakú lemezből az ábra szerint kivágunk három darab, \(\displaystyle a\) oldalú, szabályos háromszög alakú részt, majd a kivágott három darabot az egyik maradék háromszögre tesszük. Hol van az így kapott idom tömegközéppontja?
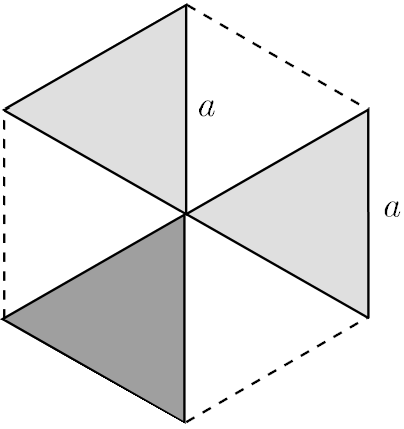
Közli: Zsigri Ferenc, Budapest
(4 pont)
A beküldési határidő 2025. október 15-én LEJÁRT.
Megoldás. Ha az ábra szerint kivágunk három szabályos háromszöget a hatszögből, akkor a maradék három háromszög tömegközéppontja az eredeti hatszög középpontjában marad. Ha a kivágott három háromszöget egymásra rakjuk, akkor ezek tömegközéppontja egyetlen szabályos háromszög súlypontjában marad, ami a szabályos háromszög bármely csúcspontjától \(\displaystyle \tfrac{2}{3}\,\cdot\,\tfrac{\sqrt{3}}{2}a=\tfrac{a}{\sqrt{3}}\) távolságra van. A három háromszög tömegét ebbe a pontba koncentrálhatjuk, míg a maradék három háromszögét az eredeti hatszög középpontjába. Így megállapíthatjuk, hogy a keletkezett idom kérdéses tömegközéppontja a két pontot összekötő szakasz felezőpontjában van, vagyis az eredeti hatszög középpontjától \(\displaystyle \tfrac{a}{2\sqrt{3}}\) távolságra.
Statisztika:
54 dolgozat érkezett. 4 pontot kapott: Bachman Krisztián , Balassa Ádám, Bangha Lóránt , Blaskovics Bálint, Csaba Gréta, Csabai Blanka, Csikós Attila, Fodor Bertalan Dénes, Győrffy Réka Rebeka, Hollósi Dominik, Horváth Péter, József Áron, Majer Veronika, Németh Martin, Probojcsevity Iván, Sógor-Jász Soma, Steib Miklós, Szabó Jázmin, Szabó Zsombor, Szighardt Anna, Tasnádi Bendegúz, Tóth Domonkos, Török Ákos, Vincze Blanka Anna. 3 pontot kapott: Börcsök Péter, Kovács Artúr-Lehel, Lukács Kristóf Pál, Medgyesi András, Nagy Nóra, Schneider Viola, Sőtér Hunor Marcell, Szabó-Medve Boldizsár, Szürös Kamilla , Török Sebestyén András, Trellák András Benedek, Vígh Attila , Zsilák Márk Péter. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 6 versenyző.
A KöMaL 2025. szeptemberi fizika feladatai

