A G. 896. feladat (2025. szeptember)

G. 896. Öt ellenállást kapcsolunk az ábra szerint egy 24 V-os feszültségforrás \(\displaystyle A\) és \(\displaystyle B\) kimenetére. Az ellenállások: \(\displaystyle R_1=40~\Omega\), \(\displaystyle R_2=50~\Omega\), \(\displaystyle R_3=R_4=10~\Omega\) és \(\displaystyle R_5=20~\Omega\).

a) Határozzuk meg az áramkör eredő ellenállását a kapcsoló zárt és nyitott állásában!

b) Mennyivel változik meg az \(\displaystyle R_4\) ellenállás teljesítménye, ha a zárt kapcsolót kinyitjuk?

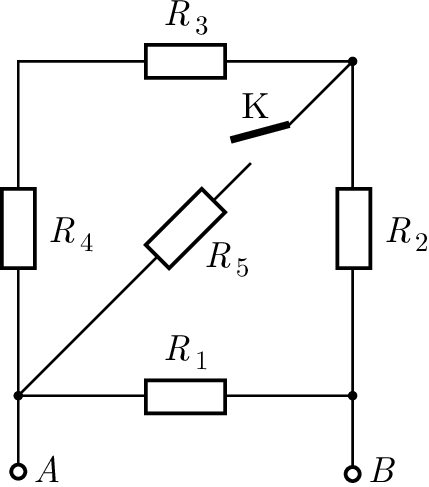
Közli: Veres Dénes, Szolnok

(4 pont)

A beküldési határidő 2025. október 15-én LEJÁRT.

Megoldás. a) Az \(\displaystyle R_3\) és az \(\displaystyle R_4\) ellenállások sorba vannak kötve, tehát ezek eredője a kettő összege, vagyis \(\displaystyle 20\,\Omega\). Ezek párhuzamosan vannak kötve (a kapcsoló zárt állása esetén) az \(\displaystyle R_5=20\,\Omega\)-os ellenállással, tehát a három ellenállás együtt \(\displaystyle 10\,\Omega\)-ot jelent, ami sorba van kötve az \(\displaystyle R_2=50\,\Omega\)-os ellenállással, tehát a négy ellenállás együtt \(\displaystyle 60\,\Omega\)-ot jelent. Ez a négy ellenállás párhuzamosan van kötve az \(\displaystyle R_1=40\,\Omega\)-os ellenállással, vagyis zárt kapcsolóállásnál az \(\displaystyle A\) és \(\displaystyle B\) pontok között az eredő ellenállás \(\displaystyle \tfrac{40\cdot60}{40+60}=24\,\Omega\).

Ha a kapcsoló nyitva van, akkor az \(\displaystyle R_2\), \(\displaystyle R_3\) és \(\displaystyle R_4\) ellenállások sorba vannak kötve, eredőjük \(\displaystyle 70\,\Omega\), és ezek vannak párhuzamosan kötve az \(\displaystyle R_1\) ellenállással. Tehát a kapcsoló nyitott állásánál (amikor az \(\displaystyle R_5\) ellenálláson nem folyik áram, akár kivehető is lehet az áramkörből) az \(\displaystyle A\) és a \(\displaystyle B\) pontok közötti eredő ellenállás \(\displaystyle \tfrac{40\cdot70}{40+70}=\tfrac{280}{11}\approx 25{,}45\,\Omega\).

b) A kapcsoló zárt állása esetén az áramkörben összesen 1 A áram folyik, hiszen a feszültség 24 V és az eredő ellenállás \(\displaystyle 24\,\Omega\). Az \(\displaystyle A\) pontból kiindulva az első csomópontnál a párhuzamos kapcsolás miatt az ellenállásokkal fordított arányban oszlik meg az áram, vagyis az \(\displaystyle R_1\) ellenálláson \(\displaystyle 0{,}6\,\mathrm{A}\), míg a másik két ágon összesen \(\displaystyle 0{,}4\,\mathrm{A}\) folyik, ami két egyenlő részre bomlik az a) részben leírtak miatt. Tehát az \(\displaystyle R_4=10\,\Omega\)-os ellenálláson \(\displaystyle 0{,}2\,\mathrm{A}\) áram folyik át, a rajta eső feszültség így 2 V, vagyis a teljesítménye a kapcsoló zárt állásánál \(\displaystyle 0{,}4\,\mathrm{W}\).

Ha kinyitjuk a kapcsolót, akkor a sorba kötött \(\displaystyle R_2\), \(\displaystyle R_3\) és \(\displaystyle R_4\) ellenállások direktben megkapják az \(\displaystyle A\) és \(\displaystyle B\) pontok 24 V-os feszültségét, ami az ellenállások arányában oszlik el közöttük. Így az \(\displaystyle R_4\) ellenállásra \(\displaystyle \tfrac{10}{10+10+50}\cdot24\,\mathrm{V}=\tfrac{24}{7}\approx 3{,}43\,\mathrm{V}\) feszültség esik, ami \(\displaystyle \tfrac{24}{70}\approx 0{,}343\,\mathrm{A}\) áramot hajt rajta keresztül. Tehát a kapcsoló kinyitása után az \(\displaystyle R_4\) ellenállásra eső teljesítmény \(\displaystyle \tfrac{24\cdot 24}{7\cdot 70}\approx 1{,}176\,\mathrm{W}\), vagyis az \(\displaystyle R_4\) ellenállás teljesítménye \(\displaystyle 0{,}4\,\mathrm{W}\)-ról \(\displaystyle 1{,}176\,\mathrm{W}\)-ra nő. A növekedés \(\displaystyle 0{,}776\,\mathrm{W}\) (azaz a teljesítmény közel háromszorosára nő).

Statisztika:

49 dolgozat érkezett.
4 pontot kapott:	Bachman Krisztián , Balassa Ádám, Balogh Anna, Bangha Lóránt , Blaskovics Bálint, Börcsök Péter, Csikós Attila, Gröller Janka, Győrffy Réka Rebeka, Horváth 019 Bálint, Kelepecz Kornél Zoltán, Majer Veronika, Nagy Nóra, Németh Martin, Olláry Viktor Alex, Szabó Ábel, Szabó Jázmin, Szabó Zsombor, Szighardt Anna, Tóth Domonkos, Vincze Blanka Anna, Zsilák Márk Péter.
3 pontot kapott:	József Áron, Vígh Attila , Villant Vanda.
2 pontot kapott:	10 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	5 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. szeptemberi fizika feladatai