 |
A G. 907. feladat (2025. december) |
G. 907. Az egyenletes tömegeloszlású, \(\displaystyle m=0{,}7~\mathrm{kg}\) tömegű, \(\displaystyle ABC\) szabályos háromszög alakú lemez \(\displaystyle A\) csúcsa az ábra szerint csuklóval csatlakozik a függőleges falhoz. A háromszög vízszintes \(\displaystyle AB\) oldalának \(\displaystyle B\) végpontját egy fonál köti össze a fallal. A fonál a vízszintessel \(\displaystyle \varphi=60^\circ\)-os szöget zár be.
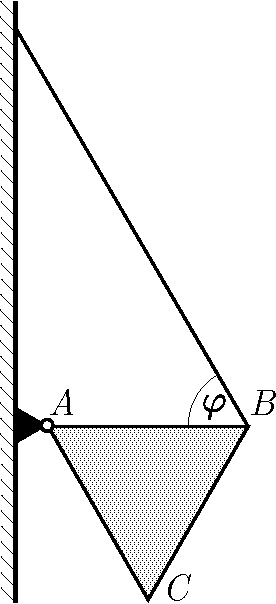
a) Mekkora erő ébred a fonálban?
b) Mekkora nagyságú, és milyen irányú erővel terheli a háromszöglemez a csuklót?
Közli: Zsigri Ferenc, Budapest
(4 pont)
A beküldési határidő 2026. január 15-én LEJÁRT.
Megoldás. A lemezre három erő hat: a nehézségi erő, a fonálerő és a csuklóerő. Ezek eredője egyensúly esetén nulla, valamint a három erő hatásvonalának egy ponton kell átmennie. (Ha ez nem így lenne, akkor bármely két erő hatásvonalának metszéspontára vizsgálva a forgatónyomatékokat a harmadik erő eredő nyomatékot képezne.) Az ábráról láthatjuk, hogy a három erő metszéspontja a \(\displaystyle C'\) pont, ami tükörszimmetrikus az \(\displaystyle AB\) szakaszra. A szimmetriából következik, hogy a fonálerő és a csuklóerő egyforma nagy, és mindkettő \(\displaystyle \varphi=60^\circ\)-os szöget zár be az \(\displaystyle AB\) szakasszal.
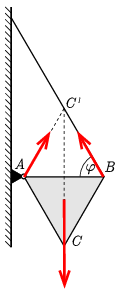
Mindkét erő nagysága
\(\displaystyle \frac{mg}{2\sin{\varphi}}=\frac{mg}{\sqrt{3}}\approx 4\,\mathrm{N}.\)
Statisztika:
40 dolgozat érkezett. 4 pontot kapott: Bachman Krisztián , Bangha Lóránt , Blaskovics Bálint, Börcsök Péter, Csikós Attila, Győrffy Réka Rebeka, Horváth Péter, Kelepecz Kornél Zoltán, Majer Veronika, Olláry Viktor Alex, Szighardt Anna, Villant Vanda, Zsilák Márk Péter. 3 pontot kapott: Balassa Ádám, Bischof Márton, Buliczka Csombor, Csabai Blanka, Horváth 019 Bálint, József Áron, Kovács Artúr-Lehel, Lukács Kristóf Pál, Németh Martin, Rácz Koppány Bendeguz, Schneider Viola, Sógor-Jász Soma, Sőtér Hunor Marcell, Sőtér Jázmin Sára, Szabó Ábel, Tóth Domonkos, Török Ákos. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2025. decemberi fizika feladatai

