Az I. 215. feladat (2009. május)

I. 215. Adott néhány kupac kavics. Minden lépésben az összes kupacból elveszünk egy kavicsot és ezekből egy új kupacot képzünk. A kupacok sorrendje nem számít.

Például:

A lépéseket addig ismételgetjük, amíg meg nem unjuk. Mivel véges a kavicsok száma, így előbb-utóbb a kavicsok eloszlása a kupacokban ciklikussá válik.

Készítsünk táblázatot, amelynek A1:Y1 tartományának első néhány cellájába bejegyezhetők a kupacok kavicsszámai. Az alatta lévő 100 sor mutassa egy-egy újabb lépés után az állapotot úgy, hogy az adott soron belül a kupacok méret szerint csökkenő sorrendben helyezkedjenek el.

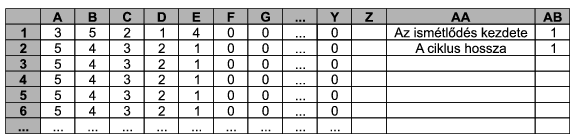
Az AB1 cellában szerepeljen, hogy hányadik lépésben kezdődik az ismétlődés, az AB2-ben pedig adjuk meg, hogy mi a ciklus hossza. Az összes kavics száma nem lehet több mint 25 (ennek ellenőrzése nem része a feladatnak). A megoldás során makró, illetve saját függvény nem használható.

Beküldendő a táblázat (i215.xls, i215.ods, ...), valamint egy rövid dokumentáció (i215.txt, i215.pdf, ...), amely tartalmazza a megoldás rövid leírását és a használt program nevét.

(A probléma azonos a januárban kitűzött I. 202. feladatéval, de most más eszközzel kell megoldani.)

(10 pont)

A beküldési határidő 2009. június 15-én LEJÁRT.

A feladat megoldása több részre bontható.

Az egyik lényeges feladat, hogy meghatározzuk a kupacok kavicsszámának sorozatát. A következő kavicssorozat mellékszámításként megkapható minden létező kupac kavicsszámának csökkentésével (A-Y oszlopok a minta számítás munkalapján), valamint egy új, az eredeti kupacok számából adódó kupac létrehozásával (Z oszlop a minta számítás munkalapján). Fontos, hogy az első sorozatot külön kell kezelni, mivel nem volt élhetünk semmilyen feltételezéssel a kupacok sorrendjét illetően. (NAGY függvény)

A következő feladat a számsorozatok kezelhetővé alakítása. Mivel itt 25 elemű tartományokat kellene vizsgálni, a könnyebb kezelhetőség érdekében praktikus ezek tartalmát egyetlen cellatartalommá összefogni. Ennek eredménye a minta ciklus munkalapján látható. (ÖSSZEFŰZ függvény) Voltak, akik nem tagolták szóközökkel számsorozatot. Ebben az esetben ez nem vezet hibához, de nagyobb kavicsszámok esetén nem biztos, hogy igazolható a helyesség.

Végül következik a ciklushossz és az ismétlődéskezdet megállapítása. A mintamegoldásban a ciklus munkalapon a B oszlopban azt vizsgáljuk, hogy az aktuális sorbeli számsorozat hányszor állt elő addig. (DARABTELI függvény)Ha ez a szám nullánál nagyobb, akkor az adott sor tartalmazza az első ismétlődést. A C oszlopban meghatározzuk, hogy az ismétlődő elem hol fordult elő először. (HOL.VAN függvény) Az első előfordulások, azaz a C oszlop értékei közül a legkisebb lesz az ismétlődés kezdete.

Az általunk készített mintamegoldás: minta215.zip

A legtöbb megoldás egyik vagy másik részfeladat leküzdése során egyedi volt. A beküldött megoldások közül Horváth Lóránd megoldását osztjuk meg az érdeklődőkkel: hl215.zip

Statisztika:

7 dolgozat érkezett.
10 pontot kapott:	Balla Attila, Horváth 135 Loránd, Kővágó Zoltán, Szabó 928 Attila.
7 pontot kapott:	2 versenyző.
3 pontot kapott:	1 versenyző.

A KöMaL 2009. májusi informatika feladatai