 |
Az I. 256. feladat (2011. január) |
I. 256. Sok természeti jelenségnél megfigyelhetők a mintázatok. Ezek általában visszavezethetők olyan folyamatokra, melyeknél a kezdetben egységes rendszerben különböző alakzatok jelennek meg. Például kémiai hullámok haladnak az oldatban, vagy az állatok bőre foltossá válik.
Készítsünk programot i256 néven, amely a foltképződést a következő modellel szimulálja. Legyen egy M×M (10
M500) négyzet, amelynek minden pontja két különböző színű állapotban lehet. Érdemes a pontok színét egy mátrixban tárolni.
A szimuláció indításakor minden pont színe véletlenszerűen a kettő közül az egyik. A továbbiakban minden lépésnél a négyzet egy véletlen pontjának a színét változtathatjuk meg. A szabály az, hogy minden pont alakuljon olyan színűvé, amilyen szomszédból több van. A változást a képernyőn jelenítjük meg anélkül, hogy a teljes négyzetet (reakcióteret) újrarajzolnánk. Ezzel a lassú képváltást, villódzást elkerülhetjük. A foltok mérete és alakja függ K (1K4) szomszédszám nagyságától.
Minta K=1, 2 illetve 3 szomszédszámra:
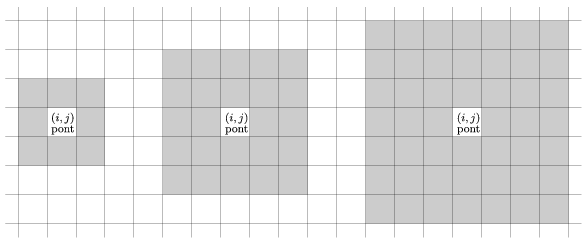
A reakciótér szélén természetesen a figyelembeveendő pontok száma kevesebb. A szimuláció addig tartson, ameddig a felhasználó le nem állítja.
A program parancssori argumentuma legyen M és K értéke.
Lehetséges eredmény M=150 és K=1 esetén
 |  |
| Feltöltött reakciótér | Szimuláció eredménye |
Beküldendő a program forráskódja (i256.pas, i256.cpp, ...), valamint a program rövid dokumentációja (i256.txt, i256.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
A beküldési határidő 2011. február 10-én LEJÁRT.
Megoldásokról
A feladatra 9 megoldás érkezett, amelyek közül 2 volt teljes értékű. Szerencsére a többivel is ki lehetett próbálni a mintázat képződés szimulációs modelljét különböző paraméterekkel. A feladat kérte, hogy „a program parancssori argumentuma legyen M és K értéke”. Ezt a futtatási üzemmódot sajnos többen nem tartották be.
Két kép M=300 és K=4 paraméterek esetén.
Röviddel idővel az indítás után...
...kicsit később...
... és egy stabilizálódott minta.
Mintamegoldásként Seres Márk Dániel (Hódmezővásárhely, Bethlen Gábor Református Gimnázium, 11. osztály) tanuló munkáját közöljük: i256.pas
Statisztika:
9 dolgozat érkezett. 10 pontot kapott: Gema Barnabás, Seres Márk Dániel. 9 pontot kapott: Barta 111 János, Szabó 928 Attila, Varga 256 Erik. 8 pontot kapott: 2 versenyző. 7 pontot kapott: 1 versenyző. 5 pontot kapott: 1 versenyző.
A KöMaL 2011. januári informatika feladatai