 |
Az I. 258. feladat (2011. január) |
I. 258. Az ókori görögök elképzelése szerint a kozmosz középpontjában a Föld foglalt helyet, a Hold, a Nap és a ,,többi'' bolygó körülötte keringett, az ég csillagai pedig egyhelyben álltak. Úgy gondolták, hogy a mozgó égitestek pályája csak tökéletes alakzat, ebben az esetben kör lehet. Azonban a legtöbb bolygó esetén megfigyelhető volt, hogy azok mozgása az égbolt állócsillagaihoz képest nem egyenletes, sőt egyes időszakokban visszafelé haladó. Ezért úgy gondolták, hogy az ilyen bolygók mozgása több kör segítségével írható le: a legegyszerűbb esetben egy Föld középpontú körön (deferens) halad egyenletesen egy másik kör (epiciklus) középpontja, és ezen második kör kerületén mozog egyenletesen a bolygó. Az alábbi ábra ezt az elképzelést szemlélteti:
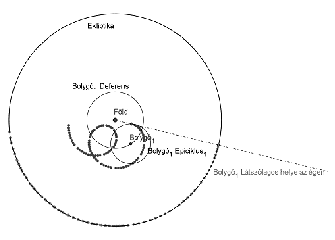
Mivel egyes bolygók valódi mozgása a mérések szerint eltért a fenti elképzeléstől, ezért további epiciklus köröket vezettek be úgy, hogy mindegyik ilyen kör középpontja az előző kerületén haladt, s a legutolsó epicikluson maga a bolygó. Több különböző sugarú és azok kerületén különböző periódusidővel haladó középpont, vagyis epiciklusok rendszerével a kor mérési lehetőségeinek pontosságát figyelembe véve helyesen kapták a bolygók mozgását.
Készítsük el két bolygó mozgásának szemléltetését a példához hasonló módon a GeoGebra (internetről ingyenesen letölthető a http://www.geogebra.org címről) számítógépes program segítségével. Mindkét bolygó esetében két epiciklus kör legyen, melyek sugara csúszka segítségével módosítható. Az egyes középpontok és a bolygók periódusideje szintén legyen csúszkával változtatható, valamint az idő múlását is így érjük el. A két bolygó valódi és látszólagos mozgását rajzoljuk ki nyomvonallal. A rajzlapon a szükséges segédpontokat és vonalakat rejtsük el, a fontos és lényeges elemeket színekkel is emeljük ki, és kapjanak érthető feliratot, tehát a kész munka legyen bemutatásra alkalmas, könnyen érthető.
Beküldendő a feladat megoldását adó i258.ggb GeoGebra állomány.
(10 pont)
A beküldési határidő 2011. február 10-én LEJÁRT.
Mintamegoldásként Kocsis Mátyás munkáját i258.ggb és Varga Erik i258(2).ggb megoldását adjuk közre. Az első külső formáját tekintve igényesebb, de nem olyan szép, hogy az animáció több változóval történik. A második megoldás jobban tükrözi a "valóságot", mert egy idő paramétertől függ a teljes mozgás.
Statisztika:
7 dolgozat érkezett. 10 pontot kapott: Kocsis 789 Mátyás, Varga 256 Erik. 9 pontot kapott: Seres Márk Dániel. 8 pontot kapott: 1 versenyző. 7 pontot kapott: 1 versenyző. 5 pontot kapott: 2 versenyző.
A KöMaL 2011. januári informatika feladatai
