Az I. 298. feladat (2012. szeptember)

I. 298. Adott egy N×N-es négyzet alakú biliárdasztal, amelynek szélén a golyók tökéletesen rugalmasan ütközhetnek. A golyók kiterjedés nélküliek és kezdetben az asztal egész koordinátájú pontjaiban állhatnak.

Készítsünk programot i298 néven, amely megadja és a standard kimenetre kiírja, hogy egy adott (k;l) koordinátájú pontból gurítva egy golyót, azzal egy másik adott (x;y) koordinátájú golyót hányféle úton találhatunk el.

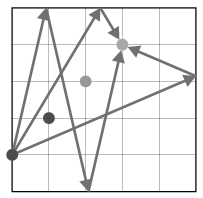
Példa három lehetséges útra

A golyó útja akkor érvényes, ha legföljebb két falon pattan vissza anélkül, hogy a megcélzott golyón kívül más golyót érintett volna. Ha egy golyó pont az asztal sarkát találja el, akkor önmagába verődik vissza, mivel ez mindkét falról történő visszapattanásnak számít. A program eredménye -- az asztal szélén történő visszapattanások száma szerint -- a kétpattanásos, az egypattanásos és a pattanás nélküli utak száma.

A program parancssori argumentuma legyen a kezdőfeltételeket leíró adatállomány neve. A fájl első sorában N (2N50) az asztal méretét, M (1<M20) a golyók számát adja meg. Az ezt követő M sor a golyók koordinátáit, majd az utolsó sor a golyóindítás (k;l) koordinátáit (1k,lN), és a célgolyó (x;y) koordinátáit írja le. A biliárdasztal bal alsó sarka legyen az (1;1) koordinátájú pont, és az első koordináta jobbra, a második koordináta felfelé nő.

Példa (lásd az ábrát):

Beküldendő a program forráskódja (i298.pas, i298.cpp, ...) és rövid dokumentációja (i298.txt, i298.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2012. október 10-én LEJÁRT.

Megoldásokról

Fényes Balázs 10. évfolyamos versenyző (Budapest, Szerb Antal Gimnázium) rövid értelmezése alapján:

A rajzokon a (k;l) koordinátákkal megadott golyót - vagyis amelyet elgurítunk - kék színnel jelöltem. Az (x;y) koordinátájú golyót - vagyis amelyiket el kell találnunk - pedig pirossal.

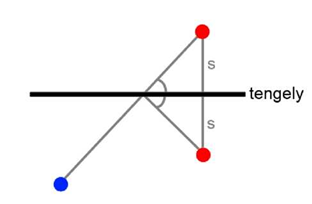
A kék golyó útvonalát könnyebben elképzelhetjük akkor, amikor a falról visszapattan, ha a piros golyót tükrözzük arra a falra, amelynek a kék golyó nekiütközött. Azaz készítünk egy tengelyes tükrözést, ahol a fal a tengely.

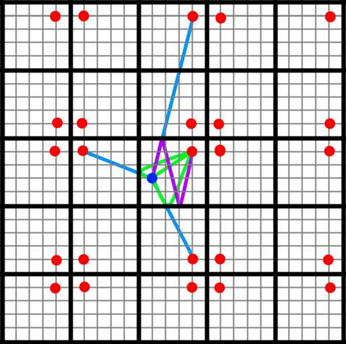
Mivel a kék golyó legfeljebb 2-szer pattanhat, ezért képzeljünk el egy 5x5 darab biliárdasztalt egymás mellé rakva az ábra szerint úgy, hogy középen van a középső asztal a kék golyót is tartalmazó eredeti; a többi asztalt úgy rakjuk le mellé, hogy a már lerakott asztalhoz képest tengelyesen tükrözött legyen, a tengely pedig az asztalok érintkező széle.

Az ábrára berajzoltam néhány lehetséges útvonalat.

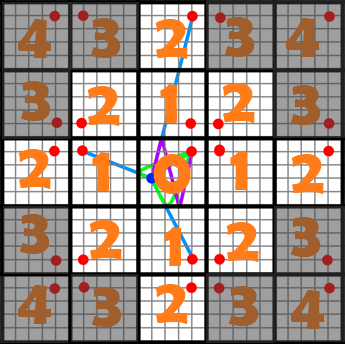
Ha megszámoljuk, hogy az egyes billiárdasztalra való eljutáshoz hányszor kell az asztalok szélén átlépni (a sarkon való átlépés 2-nek számít, mivel ott az asztal 2 széle találkozik), akkor megtudhatjuk, hogyha nincsen más golyó az asztalon, ami akadályozná a mozgását: 1 db pattanás nélküli út, 4 db egypattanásos út, 8 db kétpattanásos út lehetséges legfeljebb. Legyen a bal alsó asztal a (x = -2;y = -2) koordinátájú. Nem kell megvizsgálni, hogy az adott asztalra elgurulhat-e a kék golyó, ha az asztal koordinátáira igaz, hogy: |x| + |y|<2

A (0;0) koordinátájú asztalhoz képest vízszintes tengely mentén tükrözöttek az olyan asztalok, melyek koordinátájának y értéke páratlan, és függőleges tengely mentén tükrözöttek az olyan asztalok, melyek koordinátájának x értéke páratlan.

Ha azt vizsgáljuk, hogy az (a;b) asztal piros golyóját el lehet-e találni a (0;0) kék golyójával, akkor megnézem a (0;0), (0;b), (a;b), (a;0) asztalok által meghatározott téglalap mindegyik asztalát.

Ellenőrzéskor kiszámoljuk az induló-, és célpont által meghatározott egyenes függvényének hozzárendelési szabályát. Majd a két pont közti egész x koordinátákról eldönti, hogy behelyettesítve, rácsponton megy-e át.

Mintamegoldás:

Fényes Balázs 10. évfolyamos tanuló (Budapest, Szerb Antal Gimnázium) i298.cs

Gema Barnabás 12. évfolyamos tanuló (Veszprém, Lovassy László Gimnázium) i298.pas

Jákli Aida Karolina 10. évfolyamos tanuló (Zalaegerszeg, Zrínyi Miklós Gimnázium) Module1.vb

Statisztika:

11 dolgozat érkezett.
10 pontot kapott:	Fényes Balázs, Gema Barnabás, Jákli Aida Karolina.
9 pontot kapott:	Dobos-Kovács Mihály, Németh 017 András, Qian Lívia, Tegzes Tamás.
7 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2012. szeptemberi informatika feladatai