 |
Az I. 478. feladat (2019. március) |
I. 478. Gyerekkoromban nagymamám padlásán egy furcsa szerkezetet találtam: egy hosszú csövet, amelyhez különböző helyeken ugyanolyan átmérőjű, de különböző hosszúságú csövek csatlakoztak. Senki nem tudta megmondani, hogy mire való, de így is feltaláltuk magunkat, az éppen beleillő labdákat dobáltuk bele a szomszéd gyerekekkel. Azt néztük, hogy milyen sorrendben esnek ki a különböző színű labdák a hosszú cső végén.
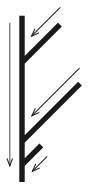
A fenti eszköz ihlette ezt a feladatot, de a labdáknak nem a színe a lényeges, hanem az, hogy milyen betűt írunk rá és azt vizsgáljuk, hogy az adott időpontokban bedobott labdák milyen szöveget adnak ki a végén. Az egyszerűség kedvéért a csövek hossza egész szám és a központi csőhöz az alsó végtől egész számnyira csatlakoznak. A központi csőhöz egy ponton csak egy cső csatlakozik. A labdák a csőben egységnyi idő alatt egységnyi utat tesznek meg. A központi csőben haladó labdának elsőbbsége van, azaz az oldalról érkező csak akkor mehet tovább, ha nem akadályozza magasabbról érkező labda. Készítsünk programot, amely a csőrendszer adatainak és a betűk csövekbe kerülési idejének ismeretében megadja a kialakuló feliratot.
A program standard bemenetének első sorában a csatlakozó csövek \(\displaystyle C\) száma és a golyók \(\displaystyle G\) száma található. A következő \(\displaystyle C\) sorban az egyes csövek hossza és a központi csőhöz való csatlakozási pontja (az alsó végétől mért távolság) szerepel, egymástól egy szóközzel elválasztva. Az ezt követő \(\displaystyle G\) sorban az angol ábécé egy betűje, a cső sorszáma és a bedobás időpontja (egész szám) található egy-egy szóközzel elválasztva. A kimenet egyetlen sora \(\displaystyle G\) darab karaktert tartalmaz: a betűket a megérkezés sorrendjében. A bemenetben a számértékek egyike sem nagyobb 1000-nél.
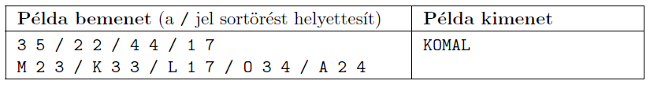
Beküldendő egy i478.zip tömörített állományban a program forráskódja és a működéséhez szükséges egyéb fájlok, továbbá a hozzá kapcsolódó dokumentáció. Utóbbi a problémamegoldás lényeges elemeire világít rá, valamint tartalmazza, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
A beküldési határidő 2019. április 10-én LEJÁRT.
A beküldött megoldások közül 3 C#, 2 C++, 1 pedig Visual Basic nyelven készült. A kézenfekvő megoldási mód a szimuláció volt. A mintabemenet mellett a tesztesetek többségénél az akadályozás vizsgálata volt a lényeges, de volt két nagyobb méretű, véletlenszerűen megadott teszteset is. i478teszt.zip
A legtömörebben megfogalmazott megoldást Horcsin Bálint készítette. I478HB.cpp I478HB.pdf
Statisztika:
6 dolgozat érkezett. 10 pontot kapott: Horcsin Bálint, Ürmössy Dorottya. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2019. márciusi informatika feladatai

