 |
Az I. 497. feladat (2019. december) |
I. 497. (É). Ebben a feladatban azt vizsgáljuk, hogy egy adott gimnáziumba jelentkező tanulók milyen eredményt értek el a felvételi vizsgán az adott városban felvételiző összes tanuló eredményéhez viszonyítva.
A felvételi vizsga írásban, két tantárgyból történik: magyarból és matematikából. Mindkét tantárgyból legfeljebb 50 pont szerezhető.
Rendelkezésünkre áll egy táblázat, amelynek első oszlopa a lehetséges pontszámokat tartalmazza 0-tól 50-ig. A mellette lévő négy oszlop pedig rendre megmutatja, hogy hány tanuló ért el ennyi pontot magyarból a városban, illetve az adott iskolában; valamint matematikából a városban, illetve az adott iskolában.
1. Töltsük be a táblázatkezelő program egyik munkalapjára az A1 cellától kezdve a felv.txt adatfájlt, majd mentsük a munkafüzetet elemzes néven a program alapértelmezett formátumában.
2. Határozzuk meg a K5:L5 tartományban, hogy hány tanuló írt felvételi dolgozatot magyarból és matematikából az adott városban, illetve az K8:L8 tartományban azt, hogy közülük hány tanuló jelentkezett az adott iskolába.
3. Határozzuk meg a K6:L6, illetve a K9:L9 tartományban a tanulók átlagos pontszámát az egyes tantárgyakból a város összes tanulója, illetve az adott iskolába jelentkező tanulók esetén. Az eredményeket két tizedesjegyre formázva jelenítsük meg.
4. Mennyivel nagyobb az adott iskolába jelentkező tanulók átlagos pontszáma, mint a város összes tanulójáé? Az eredményt képlettel írassuk tantárgyanként a K11:L11 tartományba.
5. Határozzuk meg tantárgyanként a város valamennyi felvételizője, illetve az adott iskolába jelentkező tanulók esetén is tantárgyanként, hogy melyik pontszám volt a leggyakoribb. Az eredményt képlettel adjuk meg a K7:L7, illetve a K10:L10 tartomány celláiban.
6. Szeretnénk megvizsgálni, hogy mely pontszámok fordulnak elő nagyobb gyakorisággal az adott iskolába jelentkező tanulók esetén, mint a város összes felvételizője esetén. Feltételes formázás alkalmazásával emeljük ki
\(\displaystyle a)\) a C4:D54 tartományban halványpiros háttérrel az azokhoz a pontszámokhoz tartozó sorokat, amelyekben a pontszámok relatív gyakorisága magyarból nagyobb volt az adott iskolába jelentkező tanulók esetén, mint a város összes tanulója esetén;
\(\displaystyle b)\) a G4:H54 tartományban halványzöld háttérrel az azokhoz a pontszámokhoz tartozó sorokat, amelyekben a pontszámok relatív gyakorisága matematikából nagyobb volt az adott iskolába jelentkező tanulók esetén, mint a város összes tanulója esetén.
7. Az iskola igazgatója 5 pontos sávonként is szeretné összehasonlítani az eredményeket, de csak azok az adatok érdeklik, amelyek 20 pontnál nagyobbak. Az egyes sávok alsó és felső határát az I18:J23 tartomány tartalmazza. Másolható képlet segítségével határozzuk meg a K18:K23 tartomány celláiban, hogy a tanulók hány százaléka esik az adott sávba a városban magyar felvételi vizsgát írt tanulók esetén. Hasonló módon végezzük el a számítást az adott iskolába jelentkező tanulók esetén is az L18:L23 tartományban, valamint a matematika tantárgyra vonatkozóan is az M17:N23 tartományban. Ügyeljünk arra, hogy csak a 20 pontot meghaladó tanulók képezik a mintát!
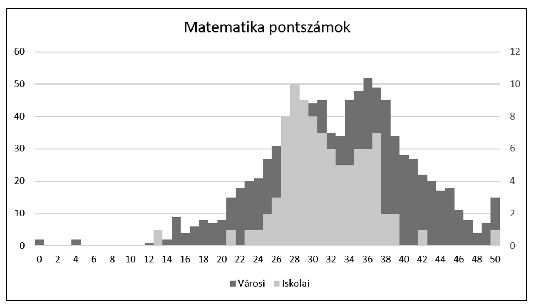
8. Ábrázoljuk csoportosított oszlopdiagramon a tanulók iskolai és városi matematika pontszámának megoszlását úgy, hogy az oszlopok érjenek össze. Az iskolai adatok áttekinthetőbb elrendezéséhez alkalmazzunk második értéktengelyt. A diagram címe ,,Matematika pontszámok'' legyen.

9. Formázzuk meg az I4:L11 tartományt a mintának megfelelően!
Beküldendő egy tömörített i497.zip állományban a megoldást adó táblázatkezelő munkafüzet és egy rövid dokumentáció, amely megadja a felhasznált táblázatkelő nevét és verzióját.
Letölthető állomány: felv.txt
(10 pont)
A beküldési határidő 2020. január 10-én LEJÁRT.
Értékelés: A feladatra 10 megoldás érkezett. A 6. feladatra többféle megoldást kaptunk, többen használtak segédcellákat, szép megoldás érkezett tömbképletek alkalmazásával, és természetesen sokan használták a SZORZATÖSSZEG függvényt is. Néhányan a 7. feladatban nem vették figyelembe (osztásnál), hogy az igazgatót "csak azok az adatok érdeklik, amelyek 20 pontnál nagyobbak", és ezzel pontot vesztettek.
Mintamegoldás: A mintamegoldás Mócsy Mátyástól, a budapesti Szent István Gimnázium 10. osztályos tanulójától származik.
Statisztika:
10 dolgozat érkezett. 10 pontot kapott: Csahók Mihály, Endrész Balázs, Horcsin Bálint, Mócsy Mátyás, Nagy 793 Márton, Ürmössy Dorottya. 9 pontot kapott: Szabó Barbara Noémi, Varga 225 Balázs. 8 pontot kapott: 2 versenyző.
A KöMaL 2019. decemberi informatika feladatai
