 |
Az I. 551. feladat (2021. december) |
I. 551. Különböző vastagságú falakat szeretnénk készíteni. Ehhez háromféle, 1, 2 és 3 cm vastagságú lapok állnak rendelkezésre.
Táblázatkezelő program segítségével oldjuk meg a falak készítéséhez használandó lapok számának és sorrendjének számításához kapcsolódó következő feladatokat.
1. Hozzuk létre a táblázatkezelőben a fal nevű állományt a program alapértelmezett formátumában.
2. Nevezzük át az első munkalapot sorrend névre.
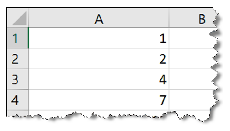
Minta a sorrend munkalaphoz
3. Határozzuk meg az A1:A60-as tartomány celláiban, hogy hányféle lényegesen különböző sorrendben lehet balról jobbra összeilleszteni a lapokat úgy, hogy a fal vastagsága az adott cella sorának értékével egyezik meg. (Lényegesen különböző a sorrend, ha az egymás után elhelyezett lapok vastagsága legalább egy helyen eltér, például 3 cm-es falvastagságnál 4 lényegesen különböző összeállítás van: \(\displaystyle 1,1,1\); \(\displaystyle 1,2\); \(\displaystyle 2,1\) és 3.)
4. Hozzuk létre a max10 nevű munkalapot és állítsuk be a mintaképen látható szürke hátterű cellákat és formátumukat.
5. Ezen munkalap B, C és D oszlopában a második sortól kezdve soroljuk fel, hogy hány 3, 2 és 1 cm-es lapot használhatunk fel a fal elkészítéséhez, ha a fal vastagságát az A2 cellába írt pozitív egész szám adja és mindhárom vastagságból legfeljebb 10–10 lapot használhatunk fel.
6. A kép A3 cellájában olvasható üzenet csak akkor jelenjen meg, ha a megadott falvastagság eléréséhez legalább egyféle lapból 10-nél több darabra lenne szükség. Ebben az esetben a többi cella maradjon üres a B–F oszlopokban a második sortól kezdve.

7. Az E oszlopban határozzuk meg, hogy az adott darabszámokból hány lényegesen különböző összeállítás lehetséges. Például 14-es falvastagság összeállítható többek között 4 db 3 cm-es és 1 db 2 centiméteres lapból. Ezek 5 lehetséges sorrendben tehetők egymás után: \(\displaystyle 3,3,3,3,2\); \(\displaystyle 3,3,3,2,3\); \(\displaystyle 3,3,2,3,3\); \(\displaystyle 3,2,3,3,3\) és \(\displaystyle 2,3,3,3,3\). Ezért ebben a sorban az E oszlopba 5 kerül, természetesen képlet felhasználásával.
8. Az F2 cellában összesítsük az E oszlopban felsorolt esetenkénti sorrendeket.
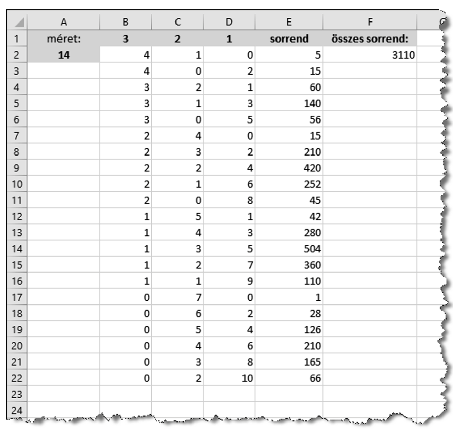
Minta a max10 munkalaphoz
Segédszámításokat mindkét munkalapon a P oszloptól kezdődően végezhetünk. A megoldáshoz makró vagy más program nem használható, csak a táblázatkezelő beépített függvényei.
Beküldendő egy i551.zip tömörített állományban a munkafüzet és egy rövid dokumentáció, amely megadja, hogy a megoldás milyen táblázatkezelő program melyik verziójában készült és egy kb. ötsoros magyarázat a megoldások módszeréről.
(10 pont)
A beküldési határidő 2022. január 17-én LEJÁRT.
Statisztika:
13 dolgozat érkezett. 10 pontot kapott: Nagy 292 Korina. 9 pontot kapott: Gyönki Dominik, Simon Tamás, Vadász Levente Márton, Zádor-Nagy Zsombor. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 0 pontot kapott: 6 versenyző.
A KöMaL 2021. decemberi informatika feladatai
