A K/C. 877. feladat (2025. november)

K/C. 877. Írjuk be az 1, 2, 3, 4, 5, 6, 7, 8, 9 számokat az ábrába úgy, hogy a három darab, négy kis háromszöget tartalmazó (a kis ábrákon szürke színű) háromszögben lévő számok szorzatát összeszorozva négyzetszámot kapjunk. Hány ilyen kitöltés van?

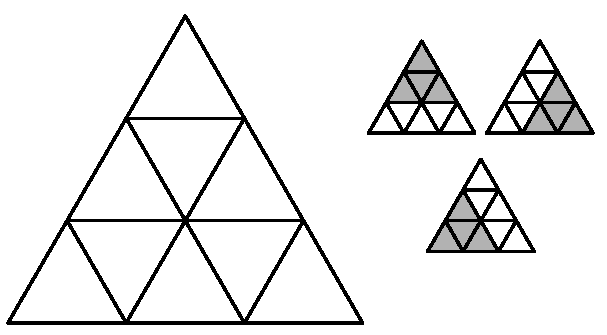
(5 pont)

A beküldési határidő 2025. december 10-én LEJÁRT.

Megoldás. Töltsük ki a kis háromszögeket az 1-es és 2-es számokkal a következőképpen:

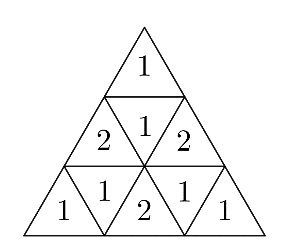
A kis háromszögekben lévő számok azt mutatják meg, hogy az adott kis háromszögbe írt szám hány részszorzatban szerepel. Azokat a számokat, amelyeket a helyette 2-vel jelölt mezőkbe írunk majd, az 1, 2, 3, 4, 5, 6, 7, 8, 9 közül tetszőlegesen választhatjuk, hiszen kétszer véve őket, a szorzatuk négyzetszám lesz. Mivel a többi hat háromszögbe írt számot csak egyszer vesszük, így meg kell keresni azt a hat számot az 1, 2, 3, 4, 5, 6, 7, 8, 9 között, melyek szorzata négyzetszám.

Az 5 és 7 nem lehet e hat szám között, mert nincs más szám 1-től 9-ig, amely 5-tel vagy 7-tel osztható.

Kérdés, hogy az 1, 2, 3, 4, 6, 8, 9 közül melyiket hagyjuk el úgy, hogy a megmaradó hat szám szorzata négyzetszám legyen?

Egy négyzetszám prímtényezős felbontásában minden prím kitevője páros szám kell, legyen, így mivel \(\displaystyle 1\cdot2\cdot3\cdot4\cdot6\cdot8\cdot9=2^7\cdot3^4\), tehát a 2-t, vagy a 8-at kell elhagyni.

Eszerint az 1-gyel jelölt mezőkbe mehet az 1, 3, 4, 6, 8, 9 és a 2-essel jelöltekbe a 2, 5, 7 vagy az 1-gyel jelölt mezőkbe mehet az 1, 2, 3, 4, 6, 9 és a 2-essel jelöltekbe az 5, 7, 8.

A hat 1-gyel jelölt mezőt 6!-féleképpen, a többi három mezőt 3!-féleképpen tölthetjük ki az oda kiválasztott számokkal. A kitöltési lehetőségek száma ezért \(\displaystyle 2\cdot6!\cdot3!=8640\).

Statisztika:

A K/C. 877. feladat értékelése még nem fejeződött be.

A KöMaL 2025. novemberi matematika feladatai