 |
A K. 158. feladat (2008. február) |
K. 158. A parkban egy négyzet alakú virágoskertet alakítanak ki négy virágágyásból (az ábrán látható módon). Egy virágágyásba csak egyféle virágot ültetnek, de az egymással szomszédos ágyásokba nem kerülhet azonos fajtájú virág (a szemköztiekbe viszont igen). A virágágyásokba kerülő virágokat háromfajta virágból választhatjuk: lehet rózsa, liliom vagy kardvirág. Hányféleképpen alakítható ki a virágoskert, ha a virágok elrendezésénél a kert tájolását is figyelembe vesszük (tehát számít, hogy melyik fajtájú virág kerül az északi, a déli, a keleti és a nyugati ágyásba)?
(6 pont)
A beküldési határidő 2008. március 10-én LEJÁRT.
Megoldás. Mivel csak háromféle virágunk van, ezért két virágágyásba azonos fajtájú virágok fognak kerülni. A feltételek miatt ezek csak szemközti ágyások lehetnek. Ennek megfelelően a virágokat három típusú elrendezésben helyezhetjük el az ágyásokban annak megfelelően, hogy mely ágyásokba kerülnek azonos fajtájú virágok:
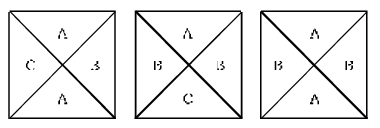
Minden esetben az A-val jelölt helyre 3-féle, a B-vel jelölt helyre 2-féle, a C-vel jelölt helyre 1-féle fajtájú virág kerülhet. Így minden esetben a lehetőségek száma 3.2=6, összesen 18. Tehát összesen 18-féleképpen alakítható ki a virágoskert.
Statisztika:
137 dolgozat érkezett. 6 pontot kapott: 95 versenyző. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 5 versenyző. 3 pontot kapott: 13 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 15 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2008. februári matematika feladatai
