A KöMaL 2008. februári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2008. március 10-én LEJÁRT. |
K. 157. A faluban az utcai lámpák egyenlő távolságban vannak elhelyezve egymástól az út mentén. Megfigyeltem, hogy 1 perc alatt pont annyit hagytam el, amennyi a sebességem 1/12-e, km/órában. Feltéve, hogy egyenletes sebességgel haladtam, és a számlálást két lámpa között félúton kezdtem és hagytam abba, milyen messze vannak egymástól a lámpák?
(6 pont)
K. 158. A parkban egy négyzet alakú virágoskertet alakítanak ki négy virágágyásból (az ábrán látható módon). Egy virágágyásba csak egyféle virágot ültetnek, de az egymással szomszédos ágyásokba nem kerülhet azonos fajtájú virág (a szemköztiekbe viszont igen). A virágágyásokba kerülő virágokat háromfajta virágból választhatjuk: lehet rózsa, liliom vagy kardvirág. Hányféleképpen alakítható ki a virágoskert, ha a virágok elrendezésénél a kert tájolását is figyelembe vesszük (tehát számít, hogy melyik fajtájú virág kerül az északi, a déli, a keleti és a nyugati ágyásba)?
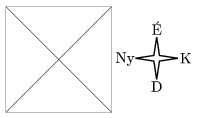
(6 pont)
K. 159. Jancsi és Juliska a metró mozgólépcsőjének aljából egyszerre indulnak el felfelé, a mozgólépcső menetirányában haladva, egyesével véve a lépcsőfokokat. (A mozgólépcső felfelé mozog egyenletes sebességgel, és a gyerekek is egyenletes sebességgel haladnak az egész mozgásuk során.) Juliska 40 másodperc alatt ér fel a lépcső tetejére, és közben 40-et lép, Jancsi 50 másodperc alatt ér fel, és közben 20-at lép. Ezután műszaki okok miatt leállítják a mozgólépcsőt, és az utasoknak gyalog kell felmenniük a már álló lépcsőn. Hányat kell lépniük, míg felérnek az aljától a tetejére, ha a lépcsőfokokat egyesével veszik?
(6 pont)
K. 160. Jancsi nagyon szeret az úgynevezett memóriajátékkal játszani. A játék 18-féle kártyából áll, mindegyikből 2-2 db van a készletben. Jancsi megkeveri a kártyákat, és kiteszi az összeset az asztalra hátlapjával felfelé. A játék fordulókból áll. Egy fordulóban megfordít az asztalon levő kártyák közül egyet, majd még egyet. Ha ezek egyformák, akkor felveszi őket, ha különbözőek, akkor visszafordítja őket. A játék addig tart, amíg minden kártyát fel nem vett az asztalról. Jancsi memóriája kiváló, ezért minden megfordított kártyáról meg tudja jegyezni, hogy melyik kártya, és hol helyezkedik el. Ilyen feltételekkel állhat-e egy-egy játék 17, 18, illetve 35 fordulóból? Ha nem, indokoljuk meg, miért nem, ha igen, adjuk meg egy-egy lehetséges játék menetét! (Feltételezzük, hogy a játék során Jancsi arra törekszik, hogy minél kevesebb lépésből álljon a játék, tehát nem forgat meg olyan kártyákat feleslegesen, melyeket már megismert.)
(6 pont)
K. 161. Adjuk össze az összes olyan pozitív egész számot, amelyet ha 2008-cal osztunk, akkor a hányados és a maradék megegyezik. Mennyi lesz az eredmény?
(6 pont)
K. 162. Az ABCD téglalap AB oldala 2 egység, AD oldala 3 egység hosszúságú. AC és CE szakaszok hossza egyenlő. Hány egységnyi hosszú a BE szakasz?
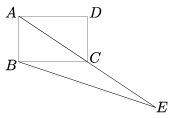
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2008. március 17-én LEJÁRT. |
C. 930. Egy társasjátékban van 11 piros, 7 kék és 20 zöld korongunk. A bank egy piros meg egy kék korongért ad két zöld korongot, egy piros meg egy zöld korongért két kék korongot, végül egy kék meg egy zöld korongért két piros korongot. A cserék során arra törekszünk, hogy csupa azonos színű korongunk legyen. Melyik ez a szín?
(5 pont)
C. 931. Adjuk meg azokat a pozitív egész számokat, amelyekből a szám jegyeinek összegét kivonva 2007-et kapunk.
(5 pont)
C. 932. Hány olyan különböző alakú háromszög van, amelyek szögeinek fokokban kifejezett mérőszámai egész számok?
(5 pont)
C. 933. Adott az ABC háromszög. Adjuk meg azt a C ponton átmenő egyenest, amelynek C-től különböző bármely D pontjára az ABD háromszög kerülete nagyobb, mint az ABC háromszög kerülete.
Javasolta: Holló Gábor (Budapest)
(5 pont)
C. 934. Három rudat (amelyeknek a vastagsága elhanyagolható) páronként merőlegesen rögzítettük egy közös pontban egymáshoz az egyik végüknél. A rudak hossza 1, 2 és 3. Az így kapott építményt úgy raktuk le az asztalra, hogy a rudak szabadon álló végei illeszkednek az asztallap síkjára. Határozzuk meg, hogy pontosan milyen magasan van a rögzítési pont az asztal fölött.
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2008. március 17-én LEJÁRT. |
B. 4062. Elhelyezhető-e a) 13, illetve b) 14 kör a síkon úgy, hogy mindegyikük közülük pontosan három másikat érintsen?
(4 pont)
B. 4063. Aladár és Béla a 81 lapos pakliból felváltva kiválasztanak egy-egy SET kártyát és leteszik az asztalra. Az veszít, aki után az asztalon szereplő kártyák között először lesz SET. Aladár kezd. Kinek van nyerő stratégiája?
(Lásd cikkünket:Variációk a SET témájára.)
Deme-Farkas Rita és Csikvári Péter
(4 pont)
B. 4064. A koordináta-rendszerben adott öt rácspont. Mutassuk meg, hogy van köztük kettő, amelyek által meghatározott szakasz felezőpontja is rácspont.
(3 pont)
B. 4065. Legyen G olyan egyszerű gráf, amelyben minden csúcs foka legalább 2. Mutassuk meg, hogy van G-nek olyan csúcsa, hogy minden belőle induló él benne van egy körben.
(3 pont)
B. 4066. Igazoljuk, hogy ha egy konvex négyszög területét mindkét középvonala felezi, akkor az paralelogramma.
(4 pont)
B. 4067. Egy k kerületű háromszög AB, BC, CA oldalaira állítsunk merőlegest rendre az A, B, C csúcsaiban. Az ezek által határolt új háromszög kerületét jelölje K. Bizonyítsuk be, hogy
ahol  ,
,  ,
,  az ABC háromszög szögei.
az ABC háromszög szögei.
(3 pont)
B. 4068. Legyenek A, B, C, a, b, c pozitív egész számok, a.b.c>1. Igazoljuk, hogy létezik olyan n pozitív egész, amelyre
A.an+B.bn+C.cn
összetett szám.
(4 pont)
B. 4069. Az A és B pontokból, rendre a és b hosszú érintők húzhatók a k körhöz. A kör egy T pontjára teljesül, hogy az A, B, T pontok nem esnek egy egyenesre és
Bizonyítsuk be, hogy az A, B, T pontokra illeszkedő kör érinti k-t.
(5 pont)
B. 4070. Az a és b természetes számok megkaphatók egymásból (10-es számrendszerben felírt) számjegyeik sorrendjének megváltoztatásával. Bizonyítsuk be, hogy
a) 2a és 2b számjegyeinek összege egyenlő.
b) Ha a és b páros számok, akkor és
számjegyeinek összege egyenlő.
Kvant feladat nyomán
(5 pont)
B. 4071. Bizonyítsuk be, hogy minden pozitív n egész számra
Javasolta: Blahota István
(4 pont)
 |
A-jelű feladatokA beküldési határidő 2008. június 16-án LEJÁRT. |
A. 446. Az A, B és C pontokból rendre a, b és c hosszú érintők húzhatók az s gömbhöz. A gömbfelület egy T pontjára, ami nincs egy síkban az A, B, C pontokkal, teljesül, hogy
Bizonyítsuk be, hogy az A, B, C, T pontokra illeszkedő gömb érinti s-et.
(5 pont)
A. 447. Igazoljuk, hogy tetszőleges a1,a2,...,an valós számokra fennáll a következő egyenlőtlenség:
(5 pont)
A. 448. Az 1,2,...,N számokat kiszíneztük 3 színnel úgy, hogy mindegyik szín legfeljebb -ször szerepel. Legyen A az ezekből képezett azon (x,y,z,w) (rendezett) számnégyeseknek a halmaza, amelyekre
és x, y, z, w azonos színű, míg B jelölje azoknak az (x,y,z,w) négyeseknek a halmazát, amelyekre
és x, y azonos színű, z, w szintén azonos színű, de a két szín különböző. Bizonyítsuk be, hogy |A|
 |B|.
|B|.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
