A K. 251. feladat (2010. március)

K. 251. Egy $\sqrt 2 -1$ oldalhosszúságú négyzet két átlóját hosszabbítsuk meg az egyik irányban annyival, amekkora a négyzet oldala.

a) Milyen hosszú a meghosszabbítások két új végpontja közötti szakasz?

b) Igazoljuk, hogy van a négyzetnek olyan csúcsa, amely a meghosszabbítások két új végpontjával egyenlő szárú háromszöget határoz meg.

(6 pont)

A beküldési határidő 2010. április 12-én LEJÁRT.

Megoldás. Használjuk az ábra jelöléseit.

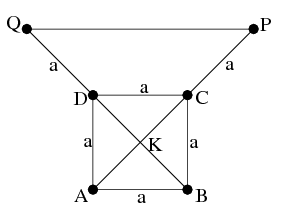
$\displaystyle a)$ Tudjuk, hogy $\displaystyle AC=\sqrt 2 a$, ezért $\displaystyle KP= \left (\frac{\sqrt 2}{2} + 1 \right )a$. Mivel $\displaystyle KPQ$ egyenlőszárú derékszögű háromszög, ezért $\displaystyle QP=\sqrt 2 \left( \frac{\sqrt 2}{2} + 1\right)a = (\sqrt 2 +1)a$. Tudjuk, hogy $\displaystyle a=\sqrt 2 -1$, így a keresett távolság: $\displaystyle QP= (\sqrt 2 +1)(\sqrt 2 -1)=1$.

$\displaystyle b)$ Mivel $\displaystyle AP=\sqrt 2 a + a =(\sqrt 2 +1)a= (\sqrt 2 +1)(\sqrt 2 -1)=1$, ezért $\displaystyle AP=QP$, vagyis $\displaystyle AQP$ egyenlőszárú háromszög. (Természetesen a szimmetria miatt $\displaystyle BPQ$ is egyenlőszárú háromszög.)

Statisztika:

120 dolgozat érkezett.

6 pontot kapott: Békési Zsuzsanna, Bingler Arnold, Bogye Balázs, Csapodi Borbála, Csóka József, Dankovics Viktor, Déri Tamás, Dóka Tamás, Domján Júlia, Drávay Zorka, Erdélyi Vivien, Erdős Szilvia, Frank Evelyn, Fülep Andrea , Girst Gábor, Hopp Norbert, Károly Péter Balázs, Katona 100 Bálint, Kedves Máté, Kelemen Bendegúz, Kertész Dávid, Keszthelyi Gergely, Leitereg András, Marx Anita, Matos Bence, Mezősi Máté, Molnár 918 Nóra, Molnár Ákos, Müller Dóra Tímea, Nagy 021 Tibor, Nagy 224 Réka, Pintér 403 Gabriella, Sárközy Kristóf, Serfőző Lőrinc, Szabó 262 Lóránt, Szentgyörgyi 994 Rita, Szeredi Levente Soma, Szilágyi Gergely Bence, Szkalisity Ábel, Takács 737 Gábor, Tóth 315 Benedek, Tóth Endre, Tóth Márton, Turányi László, Vecsernyés Tamás, Végh Dávid András, Welsz Ágnes, Wiandt Zsófia.

5 pontot kapott: 31 versenyző.

4 pontot kapott: 15 versenyző.

3 pontot kapott: 10 versenyző.

2 pontot kapott: 4 versenyző.

1 pontot kapott: 6 versenyző.

0 pontot kapott: 3 versenyző.

Nem versenyszerű: 3 dolgozat.

A KöMaL 2010. márciusi matematika feladatai

120 dolgozat érkezett.
6 pontot kapott:	Békési Zsuzsanna, Bingler Arnold, Bogye Balázs, Csapodi Borbála, Csóka József, Dankovics Viktor, Déri Tamás, Dóka Tamás, Domján Júlia, Drávay Zorka, Erdélyi Vivien, Erdős Szilvia, Frank Evelyn, Fülep Andrea , Girst Gábor, Hopp Norbert, Károly Péter Balázs, Katona 100 Bálint, Kedves Máté, Kelemen Bendegúz, Kertész Dávid, Keszthelyi Gergely, Leitereg András, Marx Anita, Matos Bence, Mezősi Máté, Molnár 918 Nóra, Molnár Ákos, Müller Dóra Tímea, Nagy 021 Tibor, Nagy 224 Réka, Pintér 403 Gabriella, Sárközy Kristóf, Serfőző Lőrinc, Szabó 262 Lóránt, Szentgyörgyi 994 Rita, Szeredi Levente Soma, Szilágyi Gergely Bence, Szkalisity Ábel, Takács 737 Gábor, Tóth 315 Benedek, Tóth Endre, Tóth Márton, Turányi László, Vecsernyés Tamás, Végh Dávid András, Welsz Ágnes, Wiandt Zsófia.
5 pontot kapott:	31 versenyző.
4 pontot kapott:	15 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	3 dolgozat.

Már regisztráltál?
Új vendég vagy?