A K. 321. feladat (2012. január)

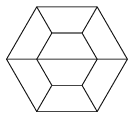
K. 321. Egy szabályos hatszög alakú asztallapot szimmetriaátlója mentén kettévágtunk, így két szimmetrikus trapéz alakú asztallapot kaptunk. A könyvtár olvasótermében ilyen trapéz alakú zöld, kék és piros asztallapok vannak. Nyolc ilyen asztallapból egy nagyobb szabályos hatszöget állítottunk össze.

a) Hányféleképpen alakíthatjuk ki ezt a formát, ha két élben szomszédos asztallap nem lehet azonos színű? (A forgatással egymásba vihető alakzatokat nem tekintjük különbözőnek.)

b) Az így összerakott hatszög körül 12-en tudnak kényelmesen leülni, mert a trapéz hosszú oldalához két szék, a többi oldalhoz csak egy-egy szék fér el. Hány darab asztallapból lehetne összerakni egy olyan nagy hatszöget, amely körül 18-an kényelmesen elférnek?

(6 pont)

A beküldési határidő 2012. február 10-én LEJÁRT.

Megoldás. a) A két középső asztal mindenképpen különböző színű. Legyen az ábrán a felső piros, az alsó kék. A legfelső asztal lehet kék vagy zöld. Ha kék, akkor az óramutató járása szerint körben haladva a szélső asztalok színe kék, zöld, piros, zöld, piros, zöld, ha pedig a legfelső szín zöld, akkor körben haladva az asztalok színe zöld, kék, a következő lehet piros vagy zöld, és így a befejezés kétféle: piros, zöld, piros, kék vagy pedig zöld, piros, zöld, kék. Tehát ebben az alapesetben háromféle megoldást találtunk. A középső két asztal színe háromféle lehet (a forgatás miatt csak az számít, hogy oda melyik két színt választottuk be), ezért a lehetőségek száma összesen 9.

b) Ha a trapéz rövidebbik oldalát egységnyinek tekintjük, akkor egy olyan hatszöget kell kiraknunk, melynek oldala nem két, hanem három egység hosszúságú. Ha elkezdjük kirakni, akkor könnyen látható, hogy egy ilyen hatszög létrehozásához 18 darab trapézra van szükségünk.

Statisztika:

138 dolgozat érkezett.
6 pontot kapott:	Bajnok Anna, Belényesi Máté, Császma Péter, Csiki 778 Nikolett, Csilling Tamás, Dombrovszky Borbála, Farkas Margit, Fekete Panna, Geiszl András, Görgei Anna Mária, Hartvig Áron, Iványi Blanka, Jójárt Alexandra, Király 719 Ágnes, Kovács 113 András, Kurucz Réka, Lengyel Ádám, Maizl Noémi, Mándoki Sára, Markó Gergely, Máthé Roland, Nagy 288 Bence, Nagy Ágnes Judit, Qian Lívia, Rátky Márton, Ruzsbánszki Nándor, Sipos-Vajda Eszter, Somogyi Zoltán, Szegedi Bálint, Szép Márton István, Szigeti Gréta Anna, Tamás Csongor, Tatár Krisztina, Tim Márton, Tóth Adrián, Tóth László Gábor, Virágh Anna, Weisz Szilvia.
4 pontot kapott:	11 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	45 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	31 versenyző.
Nem versenyszerű:	7 dolgozat.

A KöMaL 2012. januári matematika feladatai