A K. 429. feladat (2014. október)

K. 429. Az $\displaystyle ABC$ egyenlőszárú háromszög $\displaystyle C$ csúcsánál lévő szög nagysága $\displaystyle 120^\circ$. A szárfelező merőlegesek az alapot a $\displaystyle D$ és $\displaystyle E$ pontokban metszik. Mutassuk meg, hogy az $\displaystyle ABC$ háromszög területe háromszor akkora, mint a $\displaystyle CDE$ háromszög területe.

(6 pont)

A beküldési határidő 2014. november 10-én LEJÁRT.

Megoldás. Használjuk az ábra jelöléseit! Az $\displaystyle ABC$ háromszög alapon fekvő szögei $\displaystyle 30^{\circ}$-osak. A felezőmerőleges tulajdonsága miatt $\displaystyle AD = CD$ és $\displaystyle BE = EC$, tehát az $\displaystyle ACD$ és a $\displaystyle BCE$ háromszögek egyenlő szárúak, alapon fekvő szögeik nagysága $\displaystyle 30^{\circ}$. A két háromszög alapja egyenlő, szögeik is azok, tehát egybevágóak. Így száraik is egyenlőek. A $\displaystyle CD$ és $\displaystyle CE$ szakaszok egyenlősége miatt a $\displaystyle CDE$ háromszög is egyenlőszárú háromszög.

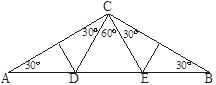
A $\displaystyle DCE$ szög nagyságát úgy kapjuk, hogy $\displaystyle 120^{\circ}$-ból kivonjuk az $\displaystyle ACD$ és $\displaystyle BCE$ szögeket, ezért a $\displaystyle DCE$ szög $\displaystyle 60^{\circ}$-os, azaz a $\displaystyle DCE$ háromszög szabályos. Az $\displaystyle ACD$ háromszöget az $\displaystyle AC$ oldalfelező merőlegese két olyan, $\displaystyle 30-60-90^{\circ}$-os háromszögre osztja, melyekből a $\displaystyle DCE$ háromszöggel egybevágó szabályos háromszög rakható össze, tehát az $\displaystyle ACD$ és $\displaystyle DCE$ háromszögek területe megegyezik. Hasonló módon megmutatható, hogy a $\displaystyle BCE$ és $\displaystyle CDE$ háromszögek területe is egyenlő, ezért az $\displaystyle ABC$ háromszög területe valóban háromszorosa a $\displaystyle CDE$ háromszög területének.

Statisztika:

110 dolgozat érkezett.
6 pontot kapott:	Béda Gergely, Csilling Eszter, Csuha Boglárka, Dévényi Dalma, Farkas Lilla, Farkas Panka, Fekete Balázs Attila, Harsányi Benedek, János Zsuzsa Anna, Járomi Bence, Kollár Johanna, Kós Anna, Kovács 124 Marcell, Kovács Marcell Dorián , Kulcsár Simon, Majzik Bendegúz Dániel, Mészáros Melinda, Mihályházi Péter, Németh 962 Ambrus, Németh Csilla Márta, Németh Levente , Oravecz Janka Éva, Orova Katinka, Öcsi Rebeka, Paulovics Péter, Rimai 217 Dániel, Sipos Fanni Emma, Sisák László Sándor, Slenker Balázs, Szalay Csilla, Szalay Gergő, Szarka Álmos, Tamási Kristóf Áron, Thuróczy Mylan, Tószegi Fanni, Valkó Bence, Varga 274 Tamás.
5 pontot kapott:	26 versenyző.
4 pontot kapott:	9 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2014. októberi matematika feladatai