A K. 439. feladat (2014. december)

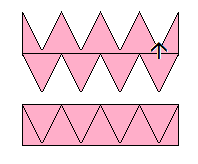
K. 439. Az ábrán látható alakzat minden oldala 10 cm hosszú, minden belső szöge \(\displaystyle 30^\circ\), \(\displaystyle 60^\circ\), \(\displaystyle 150^\circ\), vagy \(\displaystyle 300^\circ\). Mekkora a területe?

(6 pont)

A beküldési határidő 2015. január 12-én LEJÁRT.

Megoldás: A belső szögek lehetséges értékei alapján, az ábrán látható módon az alakzatba húzott szakasz szabályos háromszögeket zár be az alakzat csúcsaival.

Az így kapott „alsó” részt a „felsőbe” csúsztatva olyan téglalapot kapunk, amelynek oldalai 10 cm és 40 cm hosszúak, így területe 400 \(\displaystyle {\rm cm}^2\), ami az alakzat területével egyezik.

Statisztika:

114 dolgozat érkezett.
6 pontot kapott:	75 versenyző.
5 pontot kapott:	10 versenyző.
4 pontot kapott:	11 versenyző.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
Nem versenyszerű:	8 dolgozat.

A KöMaL 2014. decemberi matematika feladatai