A K. 460. feladat (2015. március)

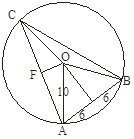
K. 460. Egy 10 egység sugarú kör középpontja az \(\displaystyle O\) pont. A körvonal három pontja (\(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\)) úgy helyezkedik el, hogy az \(\displaystyle O\) pont az \(\displaystyle ABC\) háromszög belsejében van. Tudjuk, hogy az \(\displaystyle AB\) szakasz hossza 12 egység, és az \(\displaystyle ABC\) szög nagysága \(\displaystyle 60^\circ\).

\(\displaystyle a)\) Hány egység távolságra van az \(\displaystyle O\) pont az \(\displaystyle AB\) szakasztól?

\(\displaystyle b)\) Hány egység hosszú az \(\displaystyle AC\) szakasz?

(6 pont)

A beküldési határidő 2015. április 10-én LEJÁRT.

Megoldás. a) Ha az \(\displaystyle AB\) szakasz felezőpontját összekötjük a kör középpontjával, akkor az \(\displaystyle AOB\) háromszöget két derékszögű háromszögre vágtuk szét, melyek átfogója 10, egyik befogója 6 egység hosszúságú. Pitagorasz tételével számítható, hogy a másik befogó 8 cm hosszúságú, ez tehát az \(\displaystyle O\) és az \(\displaystyle AB\) távolsága.

b) Ha az \(\displaystyle ABO\) szöget \(\displaystyle \alpha\), az \(\displaystyle OBC\) szöget pedig \(\displaystyle \beta\) jelöli, akkor \(\displaystyle AOB\angle = 180^{\circ}–2\alpha\), \(\displaystyle BOC\angle = 180^{\circ}–2\beta\), tehát \(\displaystyle AOC\angle = 2\alpha +2\beta=120^{\circ}\). Ha \(\displaystyle F\) jelöli \(\displaystyle AC\) felezőpontját, akkor az \(\displaystyle FOA\) derékszögű háromszögben \(\displaystyle FOA\angle = 60^{\circ}\), így \(\displaystyle FO\) hossza 5 egység. Szintén Pitagorasz-tétellel számítható, hogy ekkor \(\displaystyle FA = 5\sqrt3\), azaz \(\displaystyle CA = 10\sqrt3\) egység.

Statisztika:

60 dolgozat érkezett.
6 pontot kapott:	Agócs Katinka, Ágoston Tamás, Benda Orsolya, Csilling Eszter, Csuha Boglárka, Dévény Csaba, Encz Koppány, Farkas Lilla, Fekete Balázs Attila, Filip Krisztina, Harsányi Benedek, János Zsuzsa Anna, Lakatos Ágnes, Maksa Gergő, Márton Anna, Mészáros Melinda, Nagy Marcell, Németh Csilla Márta, Paulovics Péter, Péri Gergő Gábor, Pintér 345 Balázs, Posch Levente Ágoston, Rátkai Petra, Sipos Fanni Emma, Sisák László Sándor, Slenker Balázs, Szakali Benedek, Szalay Gergő, Szarka Álmos, Szűcs 865 Eszter, Tamási Kristóf Áron, Tószegi Fanni, Valkó Bence, Varga 274 Tamás, Wenczel Kata.
5 pontot kapott:	Bakó Csenge, Farkas Panka, Kóczán Kristóf, Kollár Johanna, Sziráki Boglárka Tünde.
4 pontot kapott:	2 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	11 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2015. márciusi matematika feladatai