Problem K. 836. (December 2024)

K. 836. For right triangle \(\displaystyle ABC\) point \(\displaystyle D\) is chosen on the extension of the unit length leg \(\displaystyle AB\) beyond \(\displaystyle B\) with the property \(\displaystyle BD = AC/2\). Let \(\displaystyle E\) denote the midpoint of leg \(\displaystyle AC\). The ratio of the areas of triangles \(\displaystyle AED\) and \(\displaystyle ABC\) is \(\displaystyle 2:3\). Determine the length of line segment \(\displaystyle BD\).

(5 pont)

Deadline expired on January 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tekintsük az ábrát. Jelölje \(\displaystyle BD\) hosszát \(\displaystyle x\).

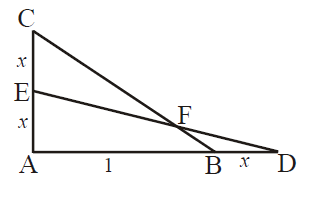
A két háromszög területének aránya:

\(\displaystyle \frac{T_{EAD}}{T_{ABC}}=\frac{0,5\cdot(1+x)\cdot x}{0,5\cdot1\cdot2x}=\frac{1+x}{2}=\frac23\), innen \(\displaystyle x=\frac13\). Tehát a \(\displaystyle BD\) szakasz hossza \(\displaystyle \frac13\) egységnyi.

Statistics:

74 students sent a solution.
5 points:	Chen Zhibo, Csík Zoltán Richárd, Dányi Janka, Fehér Ádám, Felföldi Zsófia, Fórján Bernát, Gintner Annabella , Hajdu Vince, Havasi Máté Pál, Holderith Anna, Hollósi Dominik, Huang Han, Izsa Ferenc Gergő, Jancsurák Flóra, Kalapos Szonja, Kása Richárd Zsolt, Kiss Ákos, Kondás Ádám, Koós Tamás, Kovács 444 Kamilla, Kovács Domonkos, Kudomrák Lili Anna , Kun Milán, Laczó Zoltán, Lovas Márk, Lovász Bence, Magyar Levente Árpád, Majer Veronika, Martin-Hajdu Péter, Máté Zsófia, Máthé Csongor Örs, Medgyesi András, Mixtay Mira, Molnár Levente, Mosonyi Mátyás, Nagy Alexander, Nagy-Eszlári Axel, Némethy Márk, Patócs 420 Péter, Péter Tamás, Rácz Koppány Bendeguz, Radošická Emma, Rózsa Péter, Scott Elizabeth, Škerlec Denis , Szabó Anita, Szabó Flóra, Szighardt Anna, Táborszki Réka, Zsilák Márk Péter.
4 points:	7 students.
3 points:	3 students.
2 points:	2 students.
1 point:	3 students.
0 point:	3 students.
Not shown because of missing birth date or parental permission:	6 solutions.

Problems in Mathematics of KöMaL, December 2024