Problem K. 851. (March 2025)

K. 851. Divide the shape on the figure (consisting of five congruent squares) into three parts with two cuts such that the pieces can be combined together to form a rectangle in which one side is twice as long as the other.

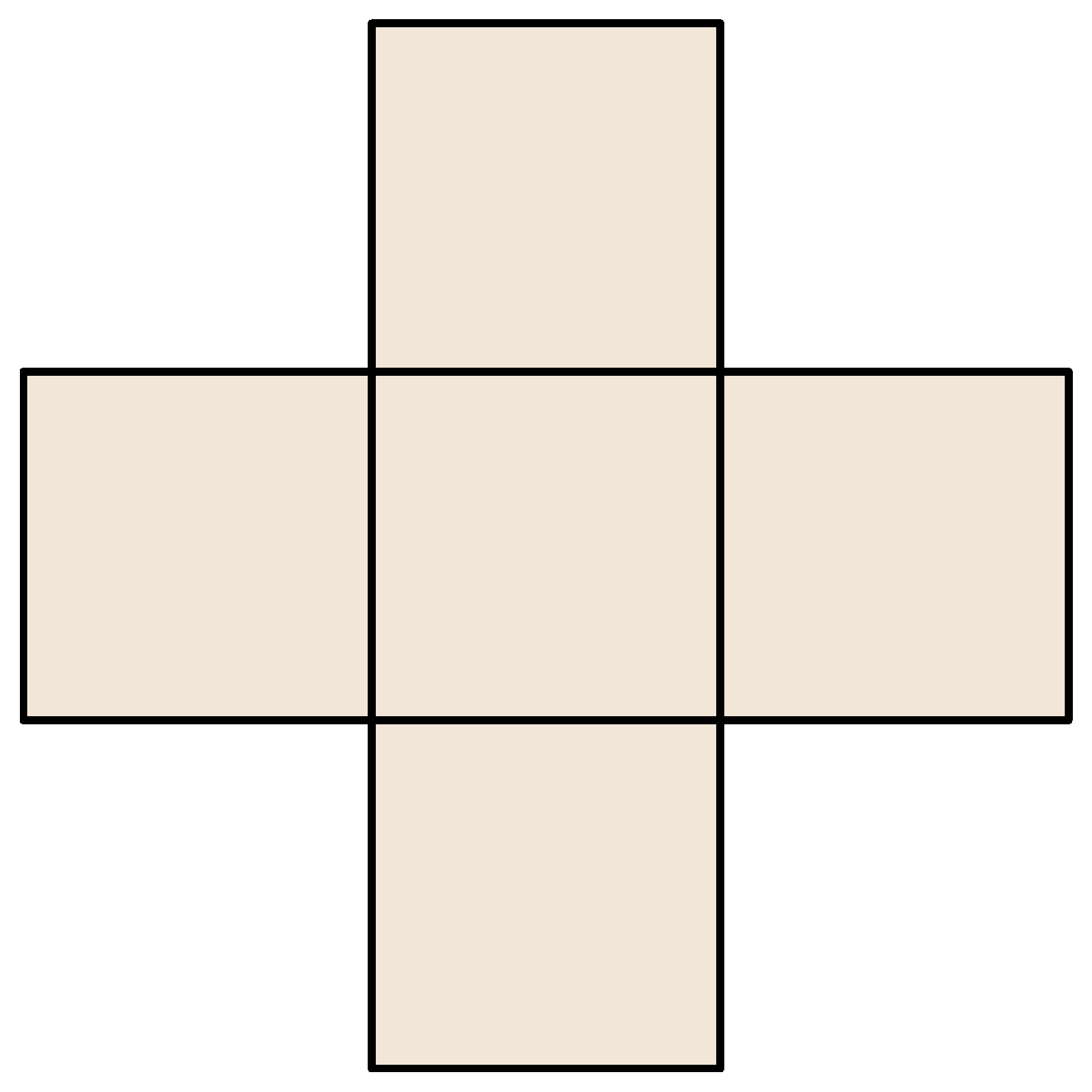
(5 pont)

Deadline expired on April 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ha a négyzet oldala 1 egység, akkor az alakzat, illetve a téglalap területe 5 egység. Legyen a téglalap egyik oldala \(\displaystyle b\), akkor a másik oldala \(\displaystyle 2b\), így \(\displaystyle 2b^2=5\). azaz \(\displaystyle b=\sqrt{2,5}\), a hosszabbik oldal pedig \(\displaystyle 2b=2\sqrt{2,5}=\sqrt{10}\). Első lépésként húzzuk be pl. a vízszintes \(\displaystyle 3\times1\)-es téglalap átlóját, mely a Pitagorasz-tétel miatt \(\displaystyle \sqrt{10}\) hosszúságú, majd megrajzolva a megfelelő erre merőleges \(\displaystyle b\) oldalt gyorsan adódik a felbontás.

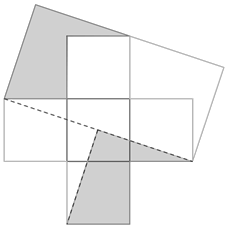
Statistics:

56 students sent a solution.
5 points:	Bloemsma Péter Sándor, Chen Zhibo, Csík Zoltán Richárd, Fórján Bernát, Győrffy Csanád, Hajdu Vince, Havasi Máté Pál, Holló Barnabás, Izsa Ferenc Gergő, Kása Richárd Zsolt, Kovács 444 Kamilla, Kovács Domonkos, Kudomrák Lili Anna , Kun Milán, Laczó Zoltán, Lovas Márk, Majer Veronika, Máté Zsófia, Mátyás Levente, Medgyesi András, Miskolczi Dóra, Molnár Levente, Nagy Alexander, Patócs 420 Péter, Péter Tamás, Radošická Emma, Rózsa Péter, Silye Zalán, Szabó Anita, Szabó Flóra, Szighardt Anna, Zsilák Márk Péter.
4 points:	Robb Horkay Jázmin, Szabó Balázs.
3 points:	1 student.
2 points:	4 students.
1 point:	4 students.
0 point:	9 students.
Not shown because of missing birth date or parental permission:	4 solutions.

Problems in Mathematics of KöMaL, March 2025