 |
A P. 4181. feladat (2009. szeptember) |
P. 4181. Az ábrán látható \(\displaystyle B=0{,}167\) T indukciójú homogén mágneses mező szélessége \(\displaystyle \ell=5\) cm. Az erővonalakra merőlegesen egy proton lép be, amely a mezőn való áthaladása után \(\displaystyle \varphi=30^\circ\)-os szögben térül el.
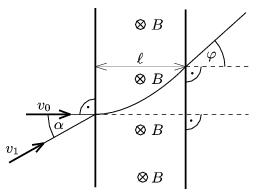
\(\displaystyle a)\) Határozzuk meg a proton \(\displaystyle v_{0}\) sebességét, illetve a mezőn való áthaladás időtartamát.
\(\displaystyle b)\) Mekkora ellenfeszültséggel lehet a protont \(\displaystyle s=10\) cm úton lefékezni, és mennyi a fékezési idő?
\(\displaystyle c)\) Tegyük fel, hogy \(\displaystyle v_{1}=2\cdot 10^6\) m/s sebességgel az ábrán látható \(\displaystyle \alpha\) szög alatt egy másik proton is érkezik. Legalább mekkora az \(\displaystyle \alpha\) szög, ha ez a részecske visszaverődik a mágneses falon?
Vermes Miklós verseny, Sopron
(5 pont)
A beküldési határidő 2009. október 12-én LEJÁRT.
\(\displaystyle {\bf Megoldás.} a)\) \(\displaystyle 1{,}6\cdot10^6~\frac{{\rm m}}{\rm s},\) illetve \(\displaystyle 3{,}3\cdot 10^{-8}~\rm s.\)
\(\displaystyle b)\) \(\displaystyle 13{,}3~\rm kV.\)
\(\displaystyle c)\) \(\displaystyle \alpha>36{,}9^\circ\).
Statisztika:
70 dolgozat érkezett. 5 pontot kapott: Balogh Gábor, Balogh Tamás, Béres Bertold, Bodnár Dávid, Budai Ádám, Csopor Dávid, Filep Gábor, Fonai Dániel, Galzó Ákos Ferenc, Garaguly Gergő, Hartstein Máté, Illés Dorottya, Janosov Milán, Knódel Máté, Kovács Attila, Kovács Benjámin, Krämer Zsolt, Kungl Ákos Ferenc, Laczkó Zoltán Balázs, Lőrincz Dóra, Molnár Alexandra, Ölvedi Balázs, Pál Domonkos, Pálovics Péter, Patartics Bálint, Pázmán Koppány, Szabó 928 Attila, Trényi Róbert, Varju 105 Tamás, Várnai Péter, Vécsey Máté, Zelei Kristóf, Zsámboki Richárd. 4 pontot kapott: Batki Bálint, Bolgár Dániel, Börcsök Bence, Burján Bence, Csóré András, Kovács 616 Philip, Kovács Attila, Köpenczei Gergő, Lájer Márton, Mayer Martin János, Neumer Tamás, Roboz Klaudia, Szikszai Lőrinc, Tamási Mátyás. 3 pontot kapott: 9 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2009. szeptemberi fizika feladatai
